Legendre sieve

Last updated November 20, 2024

In mathematics, the Legendre sieve, named after Adrien-Marie Legendre, is the simplest method in modern sieve theory. It applies the concept of the Sieve of Eratosthenes to find upper or lower bounds on the number of primes within a given set of integers. Because it is a simple extension of Eratosthenes' idea, it is sometimes called the Legendre–Eratosthenes sieve.^[1]

Legendre's identity

The central idea of the method is expressed by the following identity, sometimes called the Legendre identity:

S(A,P)=\sum _{a\in A}\sum _{d\mid a;\,d\mid P}\mu (d)=\sum _{d\mid P}\mu (d)|A_{d}|,

where A is a set of integers, P is a product of distinct primes, $\mu$ is the Möbius function, and $A_{d}$ is the set of integers in A divisible by d, and S(A, P) is defined to be:

S(A,P)=|\{n:n\in A,\gcd(n,P)=1\}|

i.e. S(A, P) is the count of numbers in A with no factors common with P.

Note that in the most typical case, A is all integers less than or equal to some real number X, P is the product of all primes less than or equal to some integer z < X, and then the Legendre identity becomes:

{\begin{aligned}S(A,P)={}&\sum _{d\mid P}\mu (d)\left\lfloor {\frac {X}{d}}\right\rfloor \\[6pt]={}&\lfloor X\rfloor -\sum _{p_{1}\leq z}\left\lfloor {\frac {X}{p_{1}}}\right\rfloor +\sum _{p_{1}<p_{2}\leq z}\left\lfloor {\frac {X}{p_{1}p_{2}}}\right\rfloor \\[4pt]&{}-\sum _{p_{1}<p_{2}<p_{3}\leq z}\left\lfloor {\frac {X}{p_{1}p_{2}p_{3}}}\right\rfloor +\cdots +\mu (P)\left\lfloor {\frac {X}{P}}\right\rfloor \end{aligned}}

(where $\lfloor X\rfloor$ denotes the floor function). In this example the fact that the Legendre identity is derived from the Sieve of Eratosthenes is clear: the first term is the number of integers below X, the second term removes the multiples of all primes, the third term adds back the multiples of two primes (which were miscounted by being "crossed out twice") but also adds back the multiples of three primes once too many, and so on until all $2^{\pi (z)}$ (where $\pi (z)$ denotes the number of primes below z) combinations of primes have been covered.

Once S(A, P) has been calculated for this special case, it can be used to bound $\pi (X)$ using the expression

S(A,P)\geq \pi (X)-\pi (z)+1,\,

which follows immediately from the definition of S(A, P).

Limitations

The Legendre sieve has a problem with fractional parts of terms accumulating into a large error, which means the sieve only gives very weak bounds in most cases. For this reason it is almost never used in practice, having been superseded by other techniques such as the Brun sieve and Selberg sieve. However, since these more powerful sieves are extensions of the basic ideas of the Legendre sieve, it is useful to first understand how this sieve works.

Related Research Articles

In number theory, an arithmetic, arithmetical, or number-theoretic function is generally any function f(n) whose domain is the positive integers and whose range is a subset of the complex numbers. Hardy & Wright include in their definition the requirement that an arithmetical function "expresses some arithmetical property of n". There is a larger class of number-theoretic functions that do not fit this definition, for example, the prime-counting functions. This article provides links to functions of both classes.

The Möbius function is a multiplicative function in number theory introduced by the German mathematician August Ferdinand Möbius in 1832. It is ubiquitous in elementary and analytic number theory and most often appears as part of its namesake the Möbius inversion formula. Following work of Gian-Carlo Rota in the 1960s, generalizations of the Möbius function were introduced into combinatorics, and are similarly denoted $.$

In mathematics, the classic Möbius inversion formula is a relation between pairs of arithmetic functions, each defined from the other by sums over divisors. It was introduced into number theory in 1832 by August Ferdinand Möbius.

In mathematics, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann.

<span class="mw-page-title-main">Quadratic reciprocity</span> Gives conditions for the solvability of quadratic equations modulo prime numbers

In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic that gives conditions for the solvability of quadratic equations modulo prime numbers. Due to its subtlety, it has many formulations, but the most standard statement is:

In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no square number other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, 10 = 2 ⋅ 5 is square-free, but 18 = 2 ⋅ 3 ⋅ 3 is not, because 18 is divisible by 9 = 3². The smallest positive square-free numbers are

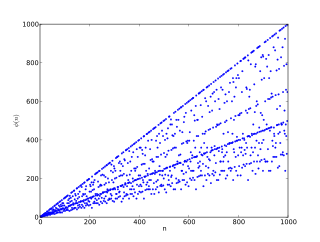
<span class="mw-page-title-main">Euler's totient function</span> Number of integers coprime to and less than n

In number theory, Euler's totient function counts the positive integers up to a given integer $n$ that are relatively prime to $n$ . It is written using the Greek letter phi as $or, and may also be called Euler's phi function . In other words, it is the number of integers k in the range 1 \leq k \leq n for which the greatest common divisor gcd(n, k) is equal to 1. The integers k of this form are sometimes referred to as totatives of n .$

In mathematics, the floor function is the function that takes as input a real number $x$ , and gives as output the greatest integer less than or equal to $x$ , denoted $⌊ x ⌋$ or $floor(x)$ . Similarly, the ceiling function maps $x$ to the least integer greater than or equal to $x$ , denoted $⌈ x ⌉$ or $ceil(x)$ .

<span class="mw-page-title-main">Root of unity</span> Number that has an integer power equal to 1

In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that yields 1 when raised to some positive integer power $n$ . Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.

In physical science and mathematics, the Legendre functions $P λ$ , $Q λ$ and associated Legendre functions $P μ λ$ , $Q μ λ$ , and Legendre functions of the second kind, $Q n$ , are all solutions of Legendre's differential equation. The Legendre polynomials and the associated Legendre polynomials are also solutions of the differential equation in special cases, which, by virtue of being polynomials, have a large number of additional properties, mathematical structure, and applications. For these polynomial solutions, see the separate Wikipedia articles.

<span class="mw-page-title-main">Prime-counting function</span> Function representing the number of primes less than or equal to a given number

In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number $x$ . It is denoted by $π (x)$ (unrelated to the number $π$ ).

<span class="mw-page-title-main">Mertens function</span> Summatory function of the Möbius function

In number theory, the Mertens function is defined for all positive integers n as

In mathematics, the polylogarithm (also known as Jonquière's function, for Alfred Jonquière) is a special function $Li s (z)$ of order $s$ and argument $z$ . Only for special values of $s$ does the polylogarithm reduce to an elementary function such as the natural logarithm or a rational function. In quantum statistics, the polylogarithm function appears as the closed form of integrals of the Fermi–Dirac distribution and the Bose–Einstein distribution, and is also known as the Fermi–Dirac integral or the Bose–Einstein integral. In quantum electrodynamics, polylogarithms of positive integer order arise in the calculation of processes represented by higher-order Feynman diagrams.

Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The prototypical example of a sifted set is the set of prime numbers up to some prescribed limit X. Correspondingly, the prototypical example of a sieve is the sieve of Eratosthenes, or the more general Legendre sieve. The direct attack on prime numbers using these methods soon reaches apparently insuperable obstacles, in the way of the accumulation of error terms. In one of the major strands of number theory in the twentieth century, ways were found of avoiding some of the difficulties of a frontal attack with a naive idea of what sieving should be.

Euclid's theorem is a fundamental statement in number theory that asserts that there are infinitely many prime numbers. It was first proven by Euclid in his work Elements. There are several proofs of the theorem.

The Meissel–Lehmer algorithm is an algorithm that computes exact values of the prime-counting function.

In number theory, the prime omega functions $and count the number of prime factors of a natural number Thereby counts each distinct prime factor, whereas the related function counts the total number of prime factors of honoring their multiplicity. That is, if we have a prime factorization of of the form for distinct primes, then the respective prime omega functions are given by and . These prime factor counting functions have many important number theoretic relations.$

The purpose of this page is to catalog new, interesting, and useful identities related to number-theoretic divisor sums, i.e., sums of an arithmetic function over the divisors of a natural number $, or equivalently the Dirichlet convolution of an arithmetic function with one:$

In analytic number theory, a Dirichlet series, or Dirichlet generating function (DGF), of a sequence is a common way of understanding and summing arithmetic functions in a meaningful way. A little known, or at least often forgotten about, way of expressing formulas for arithmetic functions and their summatory functions is to perform an integral transform that inverts the operation of forming the DGF of a sequence. This inversion is analogous to performing an inverse Z-transform to the generating function of a sequence to express formulas for the series coefficients of a given ordinary generating function.

In number theory, the real parts of the roots of unity are related to one-another by means of the minimal polynomial of $The roots of the minimal polynomial are twice the real part of the roots of unity, where the real part of a root of unity is just with coprime with$

References

↑ Iwaniec, Henryk. The sieve of Eratosthenes–Legendre. Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Sér. 4, 4 no. 2 (1977), pp. 257–268 MR 453676

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Iwaniec, Henryk. The sieve of Eratosthenes–Legendre. Annali della Scuola Normale Superiore di Pisa – Classe di Scienze, Sér. 4, 4 no. 2 (1977), pp. 257–268 MR 453676

[1]

Legendre sieve

Contents

Legendre's identity

Limitations

Related Research Articles

References