In physics, the cross section is a measure of the probability that a specific process will take place in a collision of two particles. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

In number theory, Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as or , and may also be called Euler's phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the greatest common divisor gcd(n, k) is equal to 1. The integers k of this form are sometimes referred to as totatives of n.
In mathematics, de Moivre's formula states that for any real number x and integer n it is the case that where i is the imaginary unit. The formula is named after Abraham de Moivre, although he never stated it in his works. The expression cos x + i sin x is sometimes abbreviated to cis x.
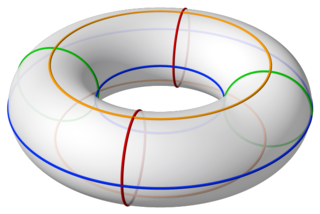
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.

In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that yields 1 when raised to some positive integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.

In geometry, the lemniscate of Bernoulli is a plane curve defined from two given points F1 and F2, known as foci, at distance 2c from each other as the locus of points P so that PF1·PF2 = c2. The curve has a shape similar to the numeral 8 and to the ∞ symbol. Its name is from lemniscatus, which is Latin for "decorated with hanging ribbons". It is a special case of the Cassini oval and is a rational algebraic curve of degree 4.
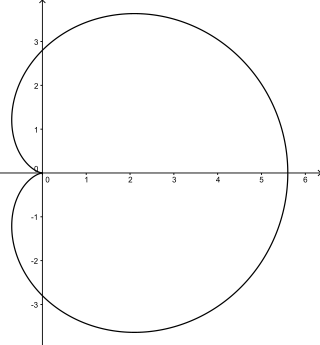
In geometry, a cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle.

In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q are not coprime. A torus knot is trivial if and only if either p or q is equal to 1 or −1. The simplest nontrivial example is the (2,3)-torus knot, also known as the trefoil knot.
In mathematics, the Lerch transcendent, is a special function that generalizes the Hurwitz zeta function and the polylogarithm. It is named after Czech mathematician Mathias Lerch, who published a paper about a similar function in 1887. The Lerch transcendent, is given by:
In probability and statistics, a circular distribution or polar distribution is a probability distribution of a random variable whose values are angles, usually taken to be in the range [0, 2π). A circular distribution is often a continuous probability distribution, and hence has a probability density, but such distributions can also be discrete, in which case they are called circular lattice distributions. Circular distributions can be used even when the variables concerned are not explicitly angles: the main consideration is that there is not usually any real distinction between events occurring at the opposite ends of the range, and the division of the range could notionally be made at any point.
The Kuramoto model, first proposed by Yoshiki Kuramoto, is a mathematical model used in describing synchronization. More specifically, it is a model for the behavior of a large set of coupled oscillators. Its formulation was motivated by the behavior of systems of chemical and biological oscillators, and it has found widespread applications in areas such as neuroscience and oscillating flame dynamics. Kuramoto was quite surprised when the behavior of some physical systems, namely coupled arrays of Josephson junctions, followed his model.

In mathematics, the lemniscate elliptic functions are elliptic functions related to the arc length of the lemniscate of Bernoulli. They were first studied by Giulio Fagnano in 1718 and later by Leonhard Euler and Carl Friedrich Gauss, among others.

Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.
There are several equivalent ways for defining trigonometric functions, and the proofs of the trigonometric identities between them depend on the chosen definition. The oldest and most elementary definitions are based on the geometry of right triangles and the ratio between their sides. The proofs given in this article use these definitions, and thus apply to non-negative angles not greater than a right angle. For greater and negative angles, see Trigonometric functions.

In knot theory, a Lissajous knot is a knot defined by parametric equations of the form
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.

Geographical distance or geodetic distance is the distance measured along the surface of the Earth, or the shortest arch length.
The Bowring series of the transverse mercator published in 1989 by Bernard Russel Bowring gave formulas for the Transverse Mercator that are simpler to program but retain millimeter accuracy.
In number theory, the real parts of the roots of unity are related to one-another by means of the minimal polynomial of The roots of the minimal polynomial are twice the real part of the roots of unity, where the real part of a root of unity is just with coprime with





































