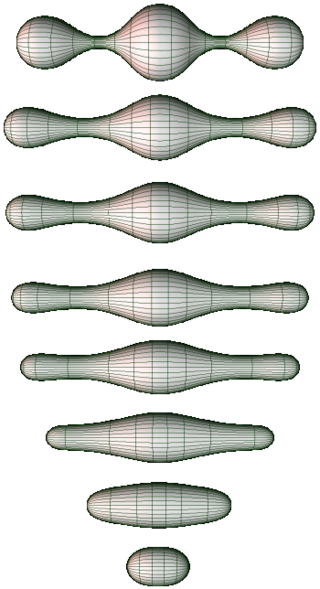
In the mathematical fields of differential geometry and geometric analysis, the Ricci flow, sometimes also referred to as Hamilton's Ricci flow, is a certain partial differential equation for a Riemannian metric. It is often said to be analogous to the diffusion of heat and the heat equation, due to formal similarities in the mathematical structure of the equation. However, it is nonlinear and exhibits many phenomena not present in the study of the heat equation.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.

In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923. In 1969, John Conway showed a version of this polynomial, now called the Alexander–Conway polynomial, could be computed using a skein relation, although its significance was not realized until the discovery of the Jones polynomial in 1984. Soon after Conway's reworking of the Alexander polynomial, it was realized that a similar skein relation was exhibited in Alexander's paper on his polynomial.
In an area of mathematics called differential topology, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere. That is, M is a sphere from the point of view of all its topological properties, but carrying a smooth structure that is not the familiar one.
In geometric topology, the Property P conjecture is a statement about 3-manifolds obtained by Dehn surgery on a knot in the 3-sphere. A knot in the 3-sphere is said to have Property P if every 3-manifold obtained by performing (non-trivial) Dehn surgery on the knot is not simply-connected. The conjecture states that all knots, except the unknot, have Property P.

In knot theory, a branch of mathematics, a knot or link in the 3-dimensional sphere is called fibered or fibred if there is a 1-parameter family of Seifert surfaces for , where the parameter runs through the points of the unit circle , such that if is not equal to then the intersection of and is exactly .
In mathematics, a 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different. There exist some topological 4-manifolds which admit no smooth structure, and even if there exists a smooth structure, it need not be unique.
In mathematics, Khovanov homology is an oriented link invariant that arises as the cohomology of a cochain complex. It may be regarded as a categorification of the Jones polynomial.
In mathematics, Floer homology is a tool for studying symplectic geometry and low-dimensional topology. Floer homology is a novel invariant that arises as an infinite-dimensional analogue of finite-dimensional Morse homology. Andreas Floer introduced the first version of Floer homology, now called symplectic Floer homology, in his proof of the Arnold conjecture in symplectic geometry. Floer also developed a closely related theory for Lagrangian submanifolds of a symplectic manifold. A third construction, also due to Floer, associates homology groups to closed three-dimensional manifolds using the Yang–Mills functional. These constructions and their descendants play a fundamental role in current investigations into the topology of symplectic and contact manifolds as well as (smooth) three- and four-dimensional manifolds.
The Tait conjectures are three conjectures made by 19th-century mathematician Peter Guthrie Tait in his study of knots. The Tait conjectures involve concepts in knot theory such as alternating knots, chirality, and writhe. All of the Tait conjectures have been solved, the most recent being the Flyping conjecture.

A slice knot is a mathematical knot in 3-dimensional space that bounds an embedded disk in 4-dimensional space.
In mathematics, more precisely in group theory and hyperbolic geometry, Arithmetic Kleinian groups are a special class of Kleinian groups constructed using orders in quaternion algebras. They are particular instances of arithmetic groups. An arithmetic hyperbolic three-manifold is the quotient of hyperbolic space by an arithmetic Kleinian group.

Tomasz Mrowka is an American mathematician specializing in differential geometry and gauge theory. He is the Singer Professor of Mathematics and former head of the Department of Mathematics at the Massachusetts Institute of Technology.

The smoothed octagon is a region in the plane found by Karl Reinhardt in 1934 and conjectured by him to have the lowest maximum packing density of the plane of all centrally symmetric convex shapes. It was also independently discovered by Kurt Mahler in 1947. It is constructed by replacing the corners of a regular octagon with a section of a hyperbola that is tangent to the two sides adjacent to the corner and asymptotic to the sides adjacent to these.

Ian Agol is an American mathematician who deals primarily with the topology of three-dimensional manifolds.

In geometry, a quadrisecant or quadrisecant line of a space curve is a line that passes through four points of the curve. This is the largest possible number of intersections that a generic space curve can have with a line, and for such curves the quadrisecants form a discrete set of lines. Quadrisecants have been studied for curves of several types:

Thomas "Tim" Daniel Cochran was a professor of mathematics at Rice University specializing in topology, especially low-dimensional topology, the theory of knots and links and associated algebra.


















