
In the mathematical field of knot theory, the bridge number is an invariant of a knot defined as the minimal number of bridges required in all the possible bridge representations of a knot.

In the mathematical field of knot theory, the bridge number is an invariant of a knot defined as the minimal number of bridges required in all the possible bridge representations of a knot.
Given a knot or link, draw a diagram of the link using the convention that a gap in the line denotes an undercrossing. Call an arc in this diagram a bridge if it includes at least one overcrossing. Then the bridge number of a knot can be found as the minimum number of bridges required for any diagram of the knot. [1] Bridge number was first studied in the 1950s by Horst Schubert. [2] [3]
The bridge number can equivalently be defined geometrically instead of topologically. In bridge representation, a knot lies entirely in the plane apart for a finite number of bridges whose projections onto the plane are straight lines. Equivalently the bridge number is the minimal number of local maxima of the projection of the knot onto a vector, where we minimize over all projections and over all conformations of the knot.
Every non-trivial knot has bridge number at least two, [1] so the knots that minimize the bridge number (other than the unknot) are the 2-bridge knots. It can be shown that every n-bridge knot can be decomposed into two trivial n-tangles and hence 2-bridge knots are rational knots.
If K is the connected sum of K1 and K2, then the bridge number of K is one less than the sum of the bridge numbers of K1 and K2. [4]

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined together so that it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of R3 upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.

In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the simple, such as a yes/no answer, to those as complex as a homology theory. Research on invariants is not only motivated by the basic problem of distinguishing one knot from another but also to understand fundamental properties of knots and their relations to other branches of mathematics.

In knot theory, a prime knot or prime link is a knot that is, in a certain sense, undecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite knots or composite links. It can be a nontrivial problem to determine whether a given knot is prime or not.

In mathematics, a knot is an embedding of a topological circle S1 in 3-dimensional Euclidean space, R3, considered up to continuous deformations (isotopies).

In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each. This construction plays a key role in the classification of closed surfaces.
In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph are linked. A flat embedding is an embedding with the property that every cycle is the boundary of a topological disk whose interior is disjoint from the graph. A linklessly embeddable graph is a graph that has a linkless or flat embedding; these graphs form a three-dimensional analogue of the planar graphs. Complementarily, an intrinsically linked graph is a graph that does not have a linkless embedding.
In knot theory, there are several competing notions of the quantity writhe, or Wr. In one sense, it is purely a property of an oriented link diagram and assumes integer values. In another sense, it is a quantity that describes the amount of "coiling" of a mathematical knot in three-dimensional space and assumes real numbers as values. In both cases, writhe is a geometric quantity, meaning that while deforming a curve in such a way that does not change its topology, one may still change its writhe.
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.
In the mathematical field of knot theory, a 2-bridge knot is a knot (mathematics)|knot which can be regular isotopy|isotoped so that the natural height function given by the z-coordinate has only two maxima and two minima as critical points. Equivalently, these are the knots with bridge number 2, the smallest possible bridge number for a nontrivial knot.

In mathematics, an immersion is a differentiable function between differentiable manifolds whose derivative is everywhere injective. Explicitly, f : M → N is an immersion if

In the mathematical field of knot theory, the tricolorability of a knot is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an isotopy invariant, and hence can be used to distinguish between two different (non-isotopic) knots. In particular, since the unknot is not tricolorable, any tricolorable knot is necessarily nontrivial.

In the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non boundary-parallel torus in its complement. Every knot is either hyperbolic, a torus, or a satellite knot. The class of satellite knots include composite knots, cable knots and Whitehead doubles. A satellite link is one that orbits a companion knot K in the sense that it lies inside a regular neighborhood of the companion.
In the mathematical subject of knot theory, the average crossing number of a knot is the result of averaging over all directions the number of crossings in a knot diagram of the knot obtained by projection onto the plane orthogonal to the direction. The average crossing number is often seen in the context of physical knot theory.
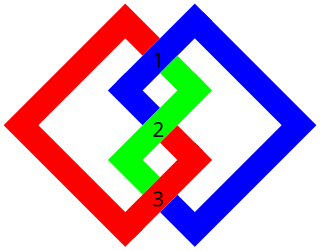
In the mathematical area of knot theory, the crossing number of a knot is the smallest number of crossings of any diagram of the knot. It is a knot invariant.
Mathematical diagrams, such as charts and graphs, are mainly designed to convey mathematical relationships—for example, comparisons over time.
In knot theory, an area of mathematics, the link group of a link is an analog of the knot group of a knot. They were described by John Milnor in his Bachelor's thesis,.

In mathematics, a tangle is generally one of two related concepts:
Jennifer Carol Schultens is an American mathematician specializing in low-dimensional topology and knot theory. She is a professor of mathematics at the University of California, Davis.