In the mathematical field of knot theory, the crosscap number of a knot K is the minimum of
taken over all compact, connected, non-orientable surfaces S bounding K; here is the Euler characteristic. The crosscap number of the unknot is zero, as the Euler characteristic of the disk is one.
The crosscap number of a knot sum is bounded:
| Hyperbolic |
|
|---|---|
| Satellite | |
| Torus | |
| Invariants | |
| Notation and operations | |
| Other | |
 | This Knot theory-related article is a stub. You can help Wikipedia by expanding it. |
In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.
In mathematics, genus has a few different, but closely related, meanings. Probably the fastest, easiest and most intuitive way to introduce genus is that it is the number of "holes" of a surface. So that a sphere has genus 0 and a torus has genus 1.
The Gauss–Bonnet theorem, or Gauss–Bonnet formula, is a relationship between surfaces in differential geometry. It connects the curvature of a surface to its Euler characteristic.
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent. It is commonly denoted by .
In mathematics, the Chern theorem states that the Euler-Poincaré characteristic of a closed even-dimensional Riemannian manifold is equal to the integral of a certain polynomial of its curvature form.
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.
In mathematics, a Seifert surface is an orientable surface whose boundary is a given knot or link.
In graph theory, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary for graph coloring on a surface of a given genus. For surfaces of genus 0, 1, 2, 3, 4, 5, 6, 7, ..., the required number of colors is 4, 7, 8, 9, 10, 11, 12, 12, .... OEIS: A000934, the chromatic number or Heawood number.
In mathematics, more specifically in the field of analytic number theory, a Landau–Siegel zero or simply Siegel zero, named after Edmund Landau and Carl Ludwig Siegel, is a type of potential counterexample to the generalized Riemann hypothesis, on the zeros of Dirichlet L-functions associated to quadratic number fields. Roughly speaking, these are possible zeros very near to s = 1.
In mathematics, the Riemann–Roch theorem for surfaces describes the dimension of linear systems on an algebraic surface. The classical form of it was first given by Castelnuovo, after preliminary versions of it were found by Max Noether (1886) and Enriques (1894). The sheaf-theoretic version is due to Hirzebruch.
In mathematics, Hopf conjecture may refer to one of several conjectural statements from differential geometry and topology attributed to Heinz Hopf.
Geometric function theory is the study of geometric properties of analytic functions. A fundamental result in the theory is the Riemann mapping theorem.
A random function – of either one variable, or two or more variables (a random field) – is called Gaussian if every finite-dimensional distribution is a multivariate normal distribution. Gaussian random fields on the sphere are useful when analysing
In the mathematical theory of knots, the stick number is a knot invariant that intuitively gives the smallest number of straight "sticks" stuck end to end needed to form a knot. Specifically, given any knot , the stick number of , denoted by , is the smallest number of edges of a polygonal path equivalent to .
In mathematics, in the field of differential geometry, the Yamabe invariant, also referred to as the sigma constant, is a real number invariant associated to a smooth manifold that is preserved under diffeomorphisms. It was first written down independently by O. Kobayashi and R. Schoen and takes its name from H. Yamabe.
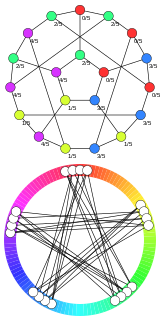
In graph theory, circular coloring is a kind of coloring that may be viewed as a refinement of the usual graph coloring. The circular chromatic number of a graph , denoted can be given by any of the following definitions, all of which are equivalent.
Anatoly Alexeyevich Karatsuba was a Russian mathematician working in the field of analytic number theory, p-adic numbers and Dirichlet series.
The graph coloring game is a mathematical game related to graph theory. Coloring game problems arose as game-theoretic versions of well-known graph coloring problems. In a coloring game, two players use a given set of colors to construct a coloring of a graph, following specific rules depending on the game we consider. One player tries to successfully complete the coloring of the graph, when the other one tries to prevent him from achieving it.
In graph theory, the act of coloring generally implies the assignment of labels to vertices, edges or faces in a graph. The incidence coloring is a special graph labeling where each incidence of an edge with a vertex is assigned a color under certain constraints.
In mathematics, a genus g surface is a surface formed by the connected sum of g many tori: the interior of a disk is removed from each of g many tori and the boundaries of the g many disks are identified, forming a g-torus. The genus of such a surface is g.
