 | This article needs attention from an expert in mathematics. The specific problem is: Description patchwork and in many places incomplete as well.(November 2008) |
![The full set of fundamental transformations and operations on 2-tangles, alongside the elementary tangles 0, [?], +-1 and +-2. Conway tangle transformations and operations.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/f/f4/Conway_tangle_transformations_and_operations.svg/600px-Conway_tangle_transformations_and_operations.svg.png)
![The trefoil knot has Conway notation [3]. Blue Trefoil Knot.png](http://upload.wikimedia.org/wikipedia/commons/thumb/b/b3/Blue_Trefoil_Knot.png/440px-Blue_Trefoil_Knot.png)
In knot theory, Conway notation, invented by John Horton Conway, is a way of describing knots that makes many of their properties clear. It composes a knot using certain operations on tangles to construct it.
In Conway notation, the tangles are generally algebraic 2-tangles. This means their tangle diagrams consist of 2 arcs and 4 points on the edge of the diagram; furthermore, they are built up from rational tangles using the Conway operations.
[The following seems to be attempting to describe only integer or 1/n rational tangles] Tangles consisting only of positive crossings are denoted by the number of crossings, or if there are only negative crossings it is denoted by a negative number. If the arcs are not crossed, or can be transformed into an uncrossed position with the Reidemeister moves, it is called the 0 or ∞ tangle, depending on the orientation of the tangle.
If a tangle, a, is reflected on the NW-SE line, it is denoted by −a. (Note that this is different from a tangle with a negative number of crossings.)Tangles have three binary operations, sum, product, and ramification, [1] however all can be explained using tangle addition and negation. The tangle product, a b, is equivalent to −a+b. and ramification or a,b, is equivalent to −a+−b.
Rational tangles are equivalent if and only if their fractions are equal. An accessible proof of this fact is given in (Kauffman and Lambropoulou 2004). A number before an asterisk, *, denotes the polyhedron number; multiple asterisks indicate that multiple polyhedra of that number exist. [2]
An integer is a number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, 5+1/2, and √2 are not.
Multiplication is one of the four elementary mathematical operations of arithmetic, with the others being addition, subtraction and division.
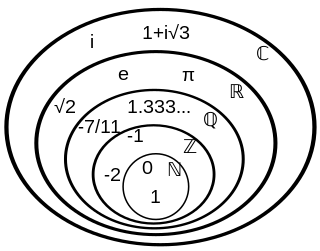
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. For being manipulated, individual numbers need to be represented by symbols, called numerals; for example, "5" is a numeral that represents the number five. As only a small number of symbols can be memorized, basic numerals are commonly organized in a numeral system, which is an organized way to represent any number. The most common numeral system is the Hindu–Arabic numeral system, which allows representing any number by a combination of ten basic numerals called digits. In addition to their use in counting and measuring, numerals are often used for labels, for ordering, and for codes. In common usage, a numeral is not clearly distinguished from the number that it represents.
Exponentiation is a mathematical operation, written as bn, involving two numbers, the baseb and the exponent or powern. When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined together so that it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of R3 upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.
Skein relations are a mathematical tool used to study knots. A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One way to answer the question is using knot polynomials, which are invariants of the knot. If two diagrams have different polynomials, they represent different knots. In general, the converse does not hold.
In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates with coefficients in another ring, often a field.
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.
In mathematics, racks and quandles are sets with binary operations satisfying axioms analogous to the Reidemeister moves used to manipulate knot diagrams.
In mathematics, Khovanov homology is an oriented link invariant that arises as the homology of a chain complex. It may be regarded as a categorification of the Jones polynomial.
In geometry, orbifold notation is a system, invented by the mathematician John Conway, for representing types of symmetry groups in two-dimensional spaces of constant curvature. The advantage of the notation is that it describes these groups in a way which indicates many of the groups' properties: in particular, it follows William Thurston in describing the orbifold obtained by taking the quotient of Euclidean space by the group under consideration.
In the mathematical field of knot theory, a 2-bridge knot is a knot which can be regular isotoped so that the natural height function given by the z-coordinate has only two maxima and two minima as critical points. Equivalently, these are the knots with bridge number 2, the smallest possible bridge number for a nontrivial knot.
In the mathematical field of knot theory, the bridge number is an invariant of a knot defined as the minimal number of bridges required in all the possible bridge representations of a knot.
In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant. An invertible link is the link equivalent of an invertible knot.
In the mathematical theory of knots, the Kontsevich invariant, also known as the Kontsevich integral of an oriented framed link, is a universal Vassiliev invariant in the sense that any coefficient of the Kontsevich invariant is of a finite type, and conversely any finite type invariant can be presented as a linear combination of such coefficients. It was defined by Maxim Kontsevich.
In mathematics, an algebraic number fieldF is a finite degree field extension of the field of rational numbers Q. Thus F is a field that contains Q and has finite dimension when considered as a vector space over Q.
In mathematics, a tangle is generally one of two related concepts:
The concept of alternating planar algebras first appeared in the work of Hernando Burgos-Soto on the Jones polynomial of alternating tangles. Alternating planar algebras provide an appropriate algebraic framework for other knot invariants in cases the elements involved in the computation are alternating. The concept has been used in extending to tangles some properties of Jones polynomial and Khovanov homology of alternating links.
| Hyperbolic |
|
|---|---|
| Satellite | |
| Torus | |
| Invariants | |
| Notation and operations | |
| Other | |
