 | This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations .(February 2013) |
This article contains a list of mathematical knots and links . See also list of knots, list of geometric topology topics.
| Hyperbolic |
|
|---|---|
| Satellite | |
| Torus | |
| Invariants | |
| Notation and operations | |
| Other | |
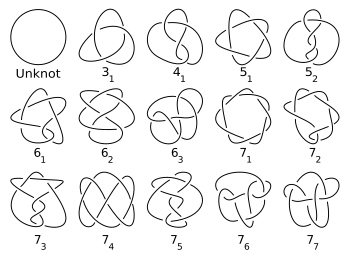
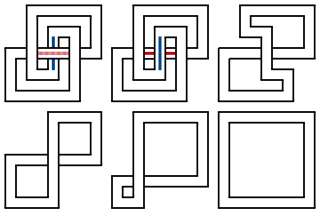In the mathematical theory of knots, the unknot, not knot, or trivial knot, is the least knotted of all knots. Intuitively, the unknot is a closed loop of rope without a knot tied into it, unknotted. To a knot theorist, an unknot is any embedded topological circle in the 3-sphere that is ambient isotopic to a geometrically round circle, the standard unknot.
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself.
In knot theory, a prime knot or prime link is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite knots or composite links. It can be a nontrivial problem to determine whether a given knot is prime or not.
In mathematics, a knot is an embedding of the circle S1 into three-dimensional Euclidean space, R3. Often two knots are considered equivalent if they are ambient isotopic, that is, if there exists a continuous deformation of R3 which takes one knot to the other.
In knot theory, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop. As the simplest knot, the trefoil is fundamental to the study of mathematical knot theory.
In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing.
In mathematical knot theory, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a trivial reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link.
In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q are not coprime. A torus knot is trivial if and only if either p or q is equal to 1 or −1. The simplest nontrivial example is the (2,3)-torus knot, also known as the trefoil knot.
In the mathematical theory of knots, a pretzel link is a special kind of link. It consists of a finite number of tangles made of two intertwined circular helices. The tangles are connected cyclicly, and the first component of the first tangle is connected to the second component of the second tangle, the first component of the second tangle is connected to the second component of the third tangle, and so on. Finally, the first component of the last tangle is connected to the second component of the first. A pretzel link which is also a knot is a pretzel knot.
In mathematical knot theory, the Hopf link is the simplest nontrivial link with more than one component. It consists of two circles linked together exactly once, and is named after Heinz Hopf.
In knot theory, a branch of topology, a Brunnian link is a nontrivial link that becomes a set of trivial unlinked circles if any one component is removed. In other words, cutting any loop frees all the other loops.
In the mathematical field of knot theory, an unlink is a link that is equivalent to finitely many disjoint circles in the plane.
In the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non boundary-parallel torus in its complement. Every knot is either hyperbolic, a torus, or a satellite knot. The class of satellite knots include composite knots, cable knots, and Whitehead doubles. A satellite link is one that orbits a companion knot K in the sense that it lies inside a regular neighborhood of the companion.
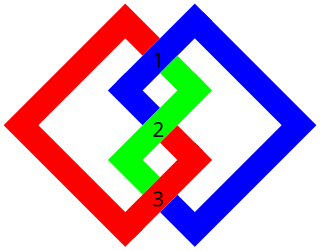
In the mathematical area of knot theory, the crossing number of a knot is the smallest number of crossings of any diagram of the knot. It is a knot invariant.
In knot theory, an area of mathematics, the link group of a link is an analog of the knot group of a knot. They were described by John Milnor in his Ph.D. thesis,. Notably, the link group is not in general the fundamental group of the link complement.
In knot theory, a branch of mathematics, a twist knot is a knot obtained by repeatedly twisting a closed loop and then linking the ends together. The twist knots are an infinite family of knots, and are considered the simplest type of knots after the torus knots.
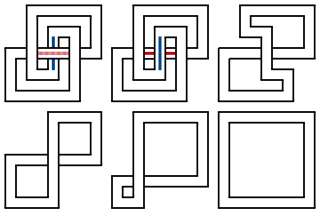
In the mathematical area of knot theory, the unknotting number of a knot is the minimum number of times the knot must be passed through itself to untie it. If a knot has unknotting number , then there exists a diagram of the knot which can be changed to unknot by switching crossings. The unknotting number of a knot is always less than half of its crossing number. This invariant was first defined by Hilmar Wendt in 1936.
In the mathematical theory of knots, L10a140 is the name in the Thistlethwaite link table of a link of three loops, which has ten crossings between the loops when presented in its simplest visual form. It is of interest because it is presumably the simplest link which possesses the Brunnian property — a link of connected components that, when one component is removed, becomes entirely unconnected — other than the six-crossing Borromean rings.
