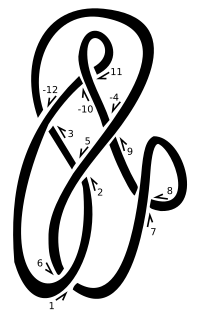In mathematics, Tait's conjecture states that "Every 3-connected planar cubic graph has a Hamiltonian cycle through all its vertices". It was proposed by P. G. Tait (1884) and disproved by W. T. Tutte (1946), who constructed a counterexample with 25 faces, 69 edges and 46 vertices. Several smaller counterexamples, with 21 faces, 57 edges and 38 vertices, were later proved minimal by Holton & McKay (1988). The condition that the graph be 3-regular is necessary due to polyhedra such as the rhombic dodecahedron, which forms a bipartite graph with six degree-four vertices on one side and eight degree-three vertices on the other side; because any Hamiltonian cycle would have to alternate between the two sides of the bipartition, but they have unequal numbers of vertices, the rhombic dodecahedron is not Hamiltonian.

Peter Guthrie Tait FRSE was a Scottish mathematical physicist and early pioneer in thermodynamics. He is best known for the mathematical physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory,
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984.,. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.

In knot theory, a knot or link diagram is alternating if the crossings alternate under, over, under, over, as one travels along each component of the link. A link is alternating if it has an alternating diagram.

Doron Zeilberger is an Israeli mathematician, known for his work in combinatorics.
In the mathematical field of knot theory, a chiral knot is a knot that is not equivalent to its mirror image. An oriented knot that is equivalent to its mirror image is an amphichiral knot, also called an achiral knot or amphicheiral knot. The chirality of a knot is a knot invariant. A knot's chirality can be further classified depending on whether or not it is invertible.
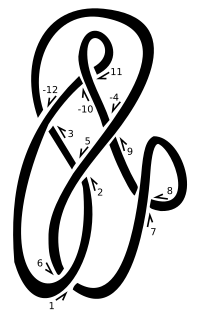
In the mathematical field of knot theory, the Dowker notation, also called the Dowker–Thistlethwaite notation or code, for a knot is a sequence of even integers. The notation is named after Clifford Hugh Dowker and Morwen Thistlethwaite, who refined a notation originally due to Peter Guthrie Tait.

In the mathematical field of knot theory, the tricolorability of a knot is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an isotopy invariant, and hence can be used to distinguish between two different (non-isotopic) knots. In particular, since the unknot is not tricolorable, any tricolorable knot is necessarily nontrivial.

In the mathematical theory of knots, the Perko pair, named after Kenneth Perko, is a pair of entries in classical knot tables that actually represent the same knot. In Dale Rolfsen's knot table, this supposed pair of distinct knots is labeled 10161 and 10162. In 1973, while working to complete the Tait–Little knot tables of knots up to 10 crossings (dating from the late 19th century), Perko found the duplication in Charles Newton Little's table. This duplication had been missed by John Horton Conway several years before in his knot table and subsequently found its way into Rolfsen's table. The Perko pair gives a counterexample to a "theorem" claimed by Little in 1900 that the writhe of a reduced diagram of a knot is an invariant (see Tait conjectures), as the two diagrams for the pair have different writhes.

Morwen B. Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory and Rubik's Cube group theory.
William W. Menasco is a topologist and a professor at the University at Buffalo. He is best known for his work in knot theory.
Clifford Hugh Dowker was a topologist known for his work in point-set topology and also for his contributions in category theory, sheaf theory and knot theory.
In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant. An invertible link is the link equivalent of an invertible knot.

Ever since Sir William Thomson's vortex theory, mathematicians have tried to classify and tabulate all possible knots. As of May 2008, all prime knots up to 16 crossings have been tabulated.

In geometric graph theory, a branch of mathematics, a polyhedral graph is the undirected graph formed from the vertices and edges of a convex polyhedron. Alternatively, in purely graph-theoretic terms, the polyhedral graphs are the 3-vertex-connected planar graphs.
In knot theory, a knot move or operation is a change or changes which preserve crossing number. Operations are used to investigate whether knots are equivalent, prime or reduced.