
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined together so that it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of R3 upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.

In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the simple, such as a yes/no answer, to those as complex as a homology theory. Research on invariants is not only motivated by the basic problem of distinguishing one knot from another but also to understand fundamental properties of knots and their relations to other branches of mathematics.
Skein relations are a mathematical tool used to study knots. A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One way to answer the question is using knot polynomials, which are invariants of the knot. If two diagrams have different polynomials, they represent different knots. In general, the converse does not hold.

In mathematics, a knot is an embedding of a topological circle S1 in 3-dimensional Euclidean space, R3, considered up to continuous deformations (isotopies).

In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each. This construction plays a key role in the classification of closed surfaces.
In the mathematical field of knot theory, the HOMFLYPT polynomial, sometimes called the generalized Jones polynomial, is a 2-variable knot polynomial, i.e. a knot invariant in the form of a polynomial of variables m and l.
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923. In 1969, John Conway showed a version of this polynomial, now called the Alexander–Conway polynomial, could be computed using a skein relation, although its significance was not realized until the discovery of the Jones polynomial in 1984. Soon after Conway's reworking of the Alexander polynomial, it was realized that a similar skein relation was exhibited in Alexander's paper on his polynomial.

In mathematical knot theory, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a trivial reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link.

In mathematics, a Seifert surface is a surface whose boundary is a given knot or link.
The Tait conjectures are three conjectures made by 19th-century mathematician Peter Guthrie Tait in his study of knots. The Tait conjectures involve concepts in knot theory such as alternating knots, chirality, and writhe. All of the Tait conjectures have been solved, the most recent being the Flyping conjecture.
In the mathematical theory of knots, a finite type invariant, or Vassiliev invariant, is a knot invariant that can be extended to an invariant of certain singular knots that vanishes on singular knots with m + 1 singularities and does not vanish on some singular knot with 'm' singularities. It is then said to be of type or order m.

In the mathematical field of knot theory, the bridge number is an invariant of a knot defined as the minimal number of bridges required in all the possible bridge representations of a knot.
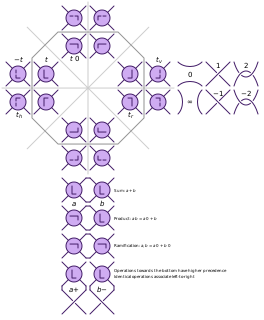
In knot theory, Conway notation, invented by John Horton Conway, is a way of describing knots that makes many of their properties clear. It composes a knot using certain operations on tangles to construct it.
Mathematical diagrams, such as charts and graphs, are mainly designed to convey mathematical relationships—for example, comparisons over time.

In combinatorial mathematics, the ménage problem or problème des ménages asks for the number of different ways in which it is possible to seat a set of male-female couples at a dining table so that men and women alternate and nobody sits next to his or her partner. This problem was formulated in 1891 by Édouard Lucas and independently, a few years earlier, by Peter Guthrie Tait in connection with knot theory. For a number of couples equal to 3, 4, 5, ... the number of seating arrangements is

In mathematics, a tangle is generally one of two related concepts:
The concept of alternating planar algebras first appeared in the work of Hernando Burgos-Soto on the Jones polynomial of alternating tangles. Alternating planar algebras provide an appropriate algebraic framework for other knot invariants in cases the elements involved in the computation are alternating. The concept has been used in extending to tangles some properties of Jones polynomial and Khovanov homology of alternating links.










