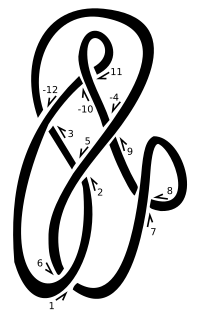Knot operation

Last updated

In knot theory, a knot move or operation is a change or changes which preserve crossing number. [1] Operations are used to investigate whether knots are equivalent, prime or reduced.

Knot theory study of mathematical knots

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined together so that it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3. Two mathematical knots are equivalent if one can be transformed into the other via a deformation of R3 upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.

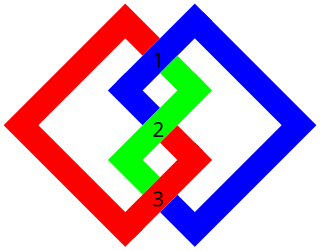
Crossing number (knot theory) integer-valued knot invariant; least number of crossings in a knot diagram

In the mathematical area of knot theory, the crossing number of a knot is the smallest number of crossings of any diagram of the knot. It is a knot invariant.

Prime knot non-trivial knot which cannot be written as the knot sum of two non-trivial knots

In knot theory, a prime knot or prime link is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite knots or composite links. It can be a nontrivial problem to determine whether a given knot is prime or not.

Knot moves or operations include the flype, Habiro move, Markov moves (I. conjugation and II. stabilization), pass move, Perko move, and Reidemeister moves (I. twist move, II. poke move, and III. slide move). [1]

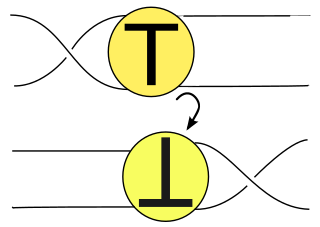
Flype

In the mathematical theory of knots, a flype is a kind of manipulation of knot and link diagrams used in the Tait flyping conjecture. It consists of twisting a part of a knot, a tangle: T by 180 degrees. Flype comes from a Scots word meaning to fold or to turn back. Two reduced alternating diagrams of an alternating link can be transformed to each other using flypes. This is the Tait flyping conjecture, proven in 1991 by Morwen Thistlethwaite and William Menasco.

Perko pair prime knot with crossing number 10; erroneously listed twice in Rolfsens table; the error was discovered by Perko

In the mathematical theory of knots, the Perko pair, named after Kenneth Perko, is a pair of entries in classical knot tables that actually represent the same knot. In Dale Rolfsen's knot table, this supposed pair of distinct knots is labeled 10161 and 10162. In 1973, while working to complete the Tait–Little knot tables of knots up to 10 crossings (dating from the late 19th century), Perko found the duplication in Charles Newton Little's table. This duplication had been missed by John Horton Conway several years before in his knot table and subsequently found its way into Rolfsen's table. The Perko pair gives a counterexample to a "theorem" claimed by Little in 1900 that the writhe of a reduced diagram of a knot is an invariant (see Tait conjectures), as the two diagrams for the pair have different writhes.

Reidemeister move one of three types of local change to a knot diagram

In the mathematical area of knot theory, a Reidemeister move is any of three local moves on a link diagram. Kurt Reidemeister (1927) and, independently, James Waddell Alexander and Garland Baird Briggs (1926), demonstrated that two knot diagrams belonging to the same knot, up to planar isotopy, can be related by a sequence of the three Reidemeister moves.

See also

Related Research Articles

Unknot loop seen as a trivial knot

The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the circle as a geometrically round circle. The unknot is also called the trivial knot. An unknot is the identity element with respect to the knot sum operation.

Knot polynomial knot invariant that is a polynomial

In the mathematical field of knot theory, a knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode some of the properties of a given knot.

Knot (mathematics) embedding of a circle in R³

In mathematics, a knot is an embedding of a circle S1 in 3-dimensional Euclidean space, R3, considered up to continuous deformations (isotopies). A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a mathematical knot. Physical properties such as friction and thickness also do not apply, although there are mathematical definitions of a knot that take such properties into account. The term knot is also applied to embeddings of S j in Sn, especially in the case j = n − 2. The branch of mathematics that studies knots is known as knot theory, and has many simple relations to graph theory.

Braid group mathematical concept in knot theory

In mathematics, the braid group on n strands, also known as the Artin braid group, is the group whose elements are equivalence classes of n-braids, and whose group operation is composition of braids. Example applications of braid groups include knot theory, where any knot may be represented as the closure of certain braids ; in mathematical physics where Artin's canonical presentation of the braid group corresponds to the Yang–Baxter equation ; and in monodromy invariants of algebraic geometry.

Geometric topology Branch of mathematics studying (smooth) functions of manifolds

In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.

A mutation is a change in the sequence of an organism's genetic material.

In knot theory, there are several competing notions of the quantity writhe, or Wr. In one sense, it is purely a property of an oriented link diagram and assumes integer values. In another sense, it is a quantity that describes the amount of "coiling" of a mathematical knot in three-dimensional space and assumes real numbers as values. In both cases, writhe is a geometric quantity, meaning that while deforming a curve in such a way that does not change its topology, one may still change its writhe.

In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984.,. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.

Alternating knot

In knot theory, a knot or link diagram is alternating if the crossings alternate under, over, under, over, as one travels along each component of the link. A link is alternating if it has an alternating diagram.

The Tait conjectures are three conjectures made by 19th-century mathematician Peter Guthrie Tait in his study of knots. The Tait conjectures involve concepts in knot theory such as alternating knots, chirality, and writhe. All of the Tait conjectures have been solved, the most recent being the Flyping conjecture.

Dowker notation

In the mathematical field of knot theory, the Dowker notation, also called the Dowker–Thistlethwaite notation or code, for a knot is a sequence of even integers. The notation is named after Clifford Hugh Dowker and Morwen Thistlethwaite, who refined a notation originally due to Peter Guthrie Tait.

Satellite knot

In the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non boundary-parallel torus in its complement. Every knot is either hyperbolic, a torus, or a satellite knot. The class of satellite knots include composite knots, cable knots and Whitehead doubles. A satellite link is one that orbits a companion knot K in the sense that it lies inside a regular neighborhood of the companion.

In knot theory, the Kauffman polynomial is a 2-variable knot polynomial due to Louis Kauffman. It is initially defined on a link diagram as

James Waddell Alexander II was a mathematician and topologist of the pre-World War II era and part of an influential Princeton topology elite, which included Oswald Veblen, Solomon Lefschetz, and others. He was one of the first members of the Institute for Advanced Study (1933–1951), and also a professor at Princeton University (1920–1951).

In the mathematical theory of knots, a Berge knot or doubly primitive knot is any member of a particular family of knots in the 3-sphere. A Berge knot K is defined by the conditions:

  1. K lies on a genus two Heegaard surface S
  2. in each handlebody bound by S, K meets some meridian disc exactly once.
Conway notation (knot theory) notation used to describe knots based on operations on tangles

In knot theory, Conway notation, invented by John Horton Conway, is a way of describing knots that makes many of their properties clear. It composes a knot using certain operations on tangles to construct it.

References

  1. 1 2 Weisstein, Eric W. "Knot Move". MathWorld .


This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.