In knot theory, a figure-eight knot is the unique knot with a crossing number of four. This makes it the knot with the third-smallest possible crossing number, after the unknot and the trefoil knot. The figure-eight knot is a prime knot.

The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the circle as a geometrically round circle. The unknot is also called the trivial knot. An unknot is the identity element with respect to the knot sum operation.
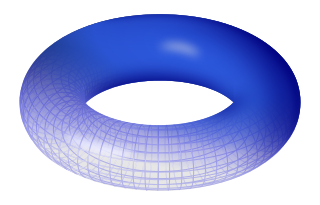
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space about an axis coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution.

In knot theory, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop. As the simplest knot, the trefoil is fundamental to the study of mathematical knot theory.

In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q are not coprime. A torus knot is trivial if and only if either p or q is equal to 1 or −1. The simplest nontrivial example is the (2,3)-torus knot, also known as the trefoil knot.

In mathematics, a Seifert surface is a surface whose boundary is a given knot or link.

In knot theory, a branch of mathematics, a knot or link in the 3-dimensional sphere is called fibered or fibred if there is a 1-parameter family of Seifert surfaces for , where the parameter runs through the points of the unit circle , such that if is not equal to then the intersection of and is exactly .

In mathematics a Padé approximant is the 'best' approximation of a function by a rational function of given order – under this technique, the approximant's power series agrees with the power series of the function it is approximating. The technique was developed around 1890 by Henri Padé, but goes back to Georg Frobenius who introduced the idea and investigated the features of rational approximations of power series.
The degree of a polynomial is the highest degree of its monomials with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. The term order has been used as a synonym of degree but, nowadays, may refer to several other concepts . For example, the polynomial which can also be expressed as has three terms. The first term has a degree of 5, the second term has a degree of 1, and the last term has a degree of 0. Therefore, the polynomial has a degree of 5, which is the highest degree of any term.

In knot theory, a Lissajous knot is a knot defined by parametric equations of the form

In knot theory, the cinquefoil knot, also known as Solomon's seal knot or the pentafoil knot, is one of two knots with crossing number five, the other being the three-twist knot. It is listed as the 51 knot in the Alexander-Briggs notation, and can also be described as the (5,2)-torus knot. The cinquefoil is the closed version of the double overhand knot.

In knot theory, the three-twist knot is the twist knot with three-half twists. It is listed as the 52 knot in the Alexander-Briggs notation, and is one of two knots with crossing number five, the other being the cinquefoil knot.

In knot theory, the stevedore knot is one of three prime knots with crossing number six, the others being the 62 knot and the 63 knot. The stevedore knot is listed as the 61 knot in the Alexander–Briggs notation, and it can also be described as a twist knot with four twists, or as the (5,−1,−1) pretzel knot.

In knot theory, the square knot is a composite knot obtained by taking the connected sum of a trefoil knot with its reflection. It is closely related to the granny knot, which is also a connected sum of two trefoils. Because the trefoil knot is the simplest nontrivial knot, the square knot and the granny knot are the simplest of all composite knots.

In knot theory, the granny knot is a composite knot obtained by taking the connected sum of two identical trefoil knots. It is closely related to the square knot, which can also be described as a connected sum of two trefoils. Because the trefoil knot is the simplest nontrivial knot, the granny knot and the square knot are the simplest of all composite knots.

In knot theory, the 62 knot is one of three prime knots with crossing number six, the others being the stevedore knot and the 63 knot. This knot is sometimes referred to as the Miller Institute knot, because it appears in the logo of the Miller Institute for Basic Research in Science at the University of California, Berkeley.

In knot theory, the 63 knot is one of three prime knots with crossing number six, the others being the stevedore knot and the 62 knot. It is alternating, hyperbolic, and fully amphichiral. It can be written as the braid word

In knot theory, a branch of mathematics, a twist knot is a knot obtained by repeatedly twisting a closed loop and then linking the ends together. The twist knots are an infinite family of knots, and are considered the simplest type of knots after the torus knots.

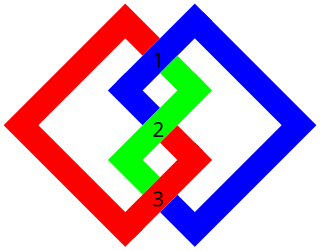
In the mathematical theory of knots, L10a140 is the name in the Thistlewaite link table of a link of three loops, which has ten crossings between the loops when presented in its simplest visual form. It is of interest because it is presumably the simplest link which possesses the Brunnian property — a link of connected components that, when one component is removed, becomes entirely unconnected — other than the six-crossing Borromean rings.