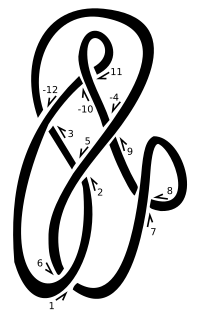In knot theory, a figure-eight knot is the unique knot with a crossing number of four. This makes it the knot with the third-smallest possible crossing number, after the unknot and the trefoil knot. The figure-eight knot is a prime knot.

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined together so that it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.

In mathematics, a knot is an embedding of a topological circle S1 in 3-dimensional Euclidean space, R3, considered up to continuous deformations (isotopies).

In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing.
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.

In mathematics, a hyperbolic link is a link in the 3-sphere with complement that has a complete Riemannian metric of constant negative curvature, i.e. has a hyperbolic geometry. A hyperbolic knot is a hyperbolic link with one component.

In knot theory, the Whitehead link, named for J. H. C. Whitehead, is one of the most basic links.
The Tait conjectures are three conjectures made by 19th-century mathematician Peter Guthrie Tait in his study of knots. The Tait conjectures involve concepts in knot theory such as alternating knots, chirality, and writhe. All of the Tait conjectures have been solved, the most recent being the Flyping conjecture.
In the mathematical field of knot theory, a split link is a link that has a (topological) 2-sphere in its complement separating one or more link components from the others. A split link is said to be splittable, and a link that is not split is called a non-split link or not splittable. Whether a link is split or non-split corresponds to whether the link complement is reducible or irreducible as a 3-manifold.
In the mathematical field of knot theory, a chiral knot is a knot that is not equivalent to its mirror image. An oriented knot that is equivalent to its mirror image is an amphichiral knot, also called an achiral knot. The chirality of a knot is a knot invariant. A knot's chirality can be further classified depending on whether or not it is invertible.
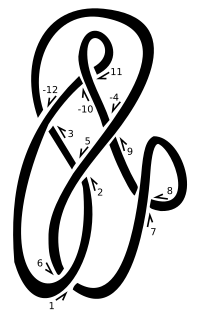
In the mathematical field of knot theory, the Dowker–Thistlethwaite (DT) notation or code, for a knot is a sequence of even integers. The notation is named after Clifford Hugh Dowker and Morwen Thistlethwaite, who refined a notation originally due to Peter Guthrie Tait.

In the mathematical field of knot theory, the hyperbolic volume of a hyperbolic link is the volume of the link's complement with respect to its complete hyperbolic metric. The volume is necessarily a finite real number, and is a topological invariant of the link. As a link invariant, it was first studied by William Thurston in connection with his geometrization conjecture.

In the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non boundary-parallel torus in its complement. Every knot is either hyperbolic, a torus, or a satellite knot. The class of satellite knots include composite knots, cable knots and Whitehead doubles. A satellite link is one that orbits a companion knot K in the sense that it lies inside a regular neighborhood of the companion.

Morwen Bernard Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory and Rubik's Cube group theory.
William W. Menasco is a topologist and a professor at the University at Buffalo. He is best known for his work in knot theory.
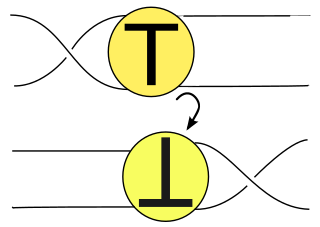
In the mathematical theory of knots, a flype is a kind of manipulation of knot and link diagrams used in the Tait flyping conjecture. It consists of twisting a part of a knot, a tangle T, by 180 degrees. Flype comes from a Scots word meaning to fold or to turn back. Two reduced alternating diagrams of an alternating link can be transformed to each other using flypes. This is the Tait flyping conjecture, proven in 1991 by Morwen Thistlethwaite and William Menasco.

Knots have been used for basic purposes such as recording information, fastening and tying objects together, for thousands of years. The early, significant stimulus in knot theory would arrive later with Sir William Thomson and his vortex theory of the atom.

Ever since Sir William Thomson's vortex theory, mathematicians have tried to classify and tabulate all possible knots. As of May 2008, all prime knots up to 16 crossings have been tabulated. The major challenge of the process is that many apparently different knots may actually be different geometrical presentations of the same topological entity, and that proving or disproving knot equivalence is much more difficult than it at first seems.
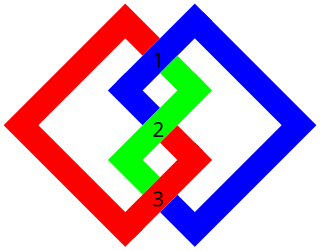
In the mathematical area of knot theory, the crossing number of a knot is the smallest number of crossings of any diagram of the knot. It is a knot invariant.