John Horton Conway was an English mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many branches of recreational mathematics, most notably the invention of the cellular automaton called the Game of Life.

In the mathematical theory of knots, the unknot, or trivial knot, is the least knotted of all knots. Intuitively, the unknot is a closed loop of rope without a knot tied into it. To a knot theorist, an unknot is any embedded topological circle in the 3-sphere that is ambient isotopic to a geometrically round circle, the standard unknot.

A Venn diagram, also called primary diagram, set diagram or logic diagram, is a diagram that shows all possible logical relations between a finite collection of different sets. These diagrams depict elements as points in the plane, and sets as regions inside closed curves. A Venn diagram consists of multiple overlapping closed curves, usually circles, each representing a set. The points inside a curve labelled S represent elements of the set S, while points outside the boundary represent elements not in the set S. This lends itself to intuitive visualizations; for example, the set of all elements that are members of both sets S and T, denoted S ∩ T and read "the intersection of S and T", is represented visually by the area of overlap of the regions S and T.

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined together so that it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.
Skein relations are a mathematical tool used to study knots. A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One way to answer the question is using knot polynomials, which are invariants of the knot. If two diagrams have different polynomials, they represent different knots. In general, the converse does not hold.

In mathematics, a knot is an embedding of a topological circle S1 in 3-dimensional Euclidean space, R3, considered up to continuous deformations (isotopies).

In knot theory, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop. As the simplest knot, the trefoil is fundamental to the study of mathematical knot theory.

In mathematics, the linking number is a numerical invariant that describes the linking of two closed curves in three-dimensional space. Intuitively, the linking number represents the number of times that each curve winds around the other. The linking number is always an integer, but may be positive or negative depending on the orientation of the two curves.

In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing.
In knot theory, there are several competing notions of the quantity writhe, or Wr. In one sense, it is purely a property of an oriented link diagram and assumes integer values. In another sense, it is a quantity that describes the amount of "coiling" of a mathematical knot in three-dimensional space and assumes real numbers as values. In both cases, writhe is a geometric quantity, meaning that while deforming a curve in such a way that does not change its topology, one may still change its writhe.
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923. In 1969, John Conway showed a version of this polynomial, now called the Alexander–Conway polynomial, could be computed using a skein relation, although its significance was not realized until the discovery of the Jones polynomial in 1984. Soon after Conway's reworking of the Alexander polynomial, it was realized that a similar skein relation was exhibited in Alexander's paper on his polynomial.

In mathematics, a hyperbolic manifold is a space where every point looks locally like hyperbolic space of some dimension. They are especially studied in dimensions 2 and 3, where they are called hyperbolic surfaces and hyperbolic 3-manifolds, respectively. In these dimensions, they are important because most manifolds can be made into a hyperbolic manifold by a homeomorphism. This is a consequence of the uniformization theorem for surfaces and the geometrization theorem for 3-manifolds proved by Perelman.
In mathematics, Floer homology is a tool for studying symplectic geometry and low-dimensional topology. Floer homology is a novel invariant that arises as an infinite-dimensional analogue of finite-dimensional Morse homology. Andreas Floer introduced the first version of Floer homology, now called Lagrangian Floer homology, in his proof of the Arnold conjecture in symplectic geometry. Floer also developed a closely related theory for Lagrangian submanifolds of a symplectic manifold. A third construction, also due to Floer, associates homology groups to closed three-dimensional manifolds using the Yang–Mills functional. These constructions and their descendants play a fundamental role in current investigations into the topology of symplectic and contact manifolds as well as (smooth) three- and four-dimensional manifolds.
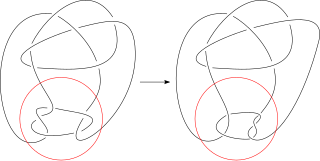
In the mathematical field of knot theory, a mutation is an operation on a knot that can produce different knots. Suppose K is a knot given in the form of a knot diagram. Consider a disc D in the projection plane of the diagram whose boundary circle intersects K exactly four times. We may suppose that the disc is geometrically round and the four points of intersection on its boundary with K are equally spaced. The part of the knot inside the disc is a tangle. There are two reflections that switch pairs of endpoints of the tangle. There is also a rotation that results from composition of the reflections. A mutation replaces the original tangle by a tangle given by any of these operations. The result will always be a knot and is called a mutant of K.
In mathematics, the unknotting problem is the problem of algorithmically recognizing the unknot, given some representation of a knot, e.g., a knot diagram. There are several types of unknotting algorithms. A major unresolved challenge is to determine if the problem admits a polynomial time algorithm; that is, whether the problem lies in the complexity class P.

In mathematics, an immersion is a differentiable function between differentiable manifolds whose derivative is everywhere injective. Explicitly, f : M → N is an immersion if

In mathematics, a tangle is generally one of two related concepts:

In geometry, a quadrisecant or quadrisecant line of a curve is a line that passes through four points of the curve. Every knotted curve in three-dimensional Euclidean space has a quadrisecant. The number of quadrisecants of an algebraic curve in complex projective space can be computed by a formula derived by Arthur Cayley. Quadrisecants of skew lines are also associated with ruled surfaces and the Schläfli double six configuration.