 | |
| Braid length | 2 |
|---|---|
| Braid no. | 2 |
| Crossing no. | 2 |
| Hyperbolic volume | 0 |
| Linking no. | 1 |
| Stick no. | 6 |
| Unknotting no. | 1 |
| Conway notation | [2] |
| A–B notation | 22 1 |
| Thistlethwaite | L2a1 |
| Last /Next | L0 / L4a1 |
| Other | |
| alternating, torus, fibered | |
In mathematical knot theory, the Hopf link is the simplest nontrivial link with more than one component. [1] It consists of two circles linked together exactly once, [2] and is named after Heinz Hopf. [3]
A concrete model consists of two unit circles in perpendicular planes, each passing through the center of the other. [2] This model minimizes the ropelength of the link and until 2002 the Hopf link was the only link whose ropelength was known. [4] The convex hull of these two circles forms a shape called an oloid. [5]
Depending on the relative orientations of the two components the linking number of the Hopf link is ±1. [6]
The Hopf link is a (2,2)-torus link [7] with the braid word [8]
The knot complement of the Hopf link is R × S1 × S1, the cylinder over a torus. [9] This space has a locally Euclidean geometry, so the Hopf link is not a hyperbolic link. The knot group of the Hopf link (the fundamental group of its complement) is Z2 (the free abelian group on two generators), distinguishing it from an unlinked pair of loops which has the free group on two generators as its group. [10]
The Hopf-link is not tricolorable: it is not possible to color the strands of its diagram with three colors, so that at least two of the colors are used and so that every crossing has one or three colors present. Each link has only one strand, and if both strands are given the same color then only one color is used, while if they are given different colors then the crossings will have two colors present.
The Hopf fibration is a continuous function from the 3-sphere (a three-dimensional surface in four-dimensional Euclidean space) into the more familiar 2-sphere, with the property that the inverse image of each point on the 2-sphere is a circle. Thus, these images decompose the 3-sphere into a continuous family of circles, and each two distinct circles form a Hopf link. This was Hopf's motivation for studying the Hopf link: because each two fibers are linked, the Hopf fibration is a nontrivial fibration. This example began the study of homotopy groups of spheres. [11]
The Hopf link is also present in some proteins. [12] [13] It consists of two covalent loops, formed by pieces of protein backbone, closed with disulfide bonds. The Hopf link topology is highly conserved in proteins and adds to their stability. [12]
The Hopf link is named after topologist Heinz Hopf, who considered it in 1931 as part of his research on the Hopf fibration. [14] However, in mathematics, it was known to Carl Friedrich Gauss before the work of Hopf. [3] It has also long been used outside mathematics, for instance as the crest of Buzan-ha, a Japanese Buddhist sect founded in the 16th century.
John Willard Milnor is an American mathematician known for his work in differential topology, algebraic K-theory and low-dimensional holomorphic dynamical systems. Milnor is a distinguished professor at Stony Brook University and one of the five mathematicians to have won the Fields Medal, the Wolf Prize, and the Abel Prize
In the mathematical field of topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing through itself.
In mathematics, and particularly topology, a fiber bundle is a space that is locally a product space, but globally may have a different topological structure. Specifically, the similarity between a space and a product space is defined using a continuous surjective map, that in small regions of behaves just like a projection from corresponding regions of to The map called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space is known as the total space of the fiber bundle, as the base space, and the fiber.
In mathematics, a knot is an embedding of the circle S1 into three-dimensional Euclidean space, R3. Often two knots are considered equivalent if they are ambient isotopic, that is, if there exists a continuous deformation of R3 which takes one knot to the other.
In knot theory, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop. As the simplest knot, the trefoil is fundamental to the study of mathematical knot theory.
In the mathematical field of differential topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle. Technically, Hopf found a many-to-one continuous function from the 3-sphere onto the 2-sphere such that each distinct point of the 2-sphere is mapped from a distinct great circle of the 3-sphere. Thus the 3-sphere is composed of fibers, where each fiber is a circle — one for each point of the 2-sphere.
In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing.
In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting about their precise geometry. Unlike homology groups, which are also topological invariants, the homotopy groups are surprisingly complex and difficult to compute.
In mathematical knot theory, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory. Implicit in this definition is that there is a trivial reference link, usually called the unlink, but the word is also sometimes used in context where there is no notion of a trivial link.
In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q are not coprime. A torus knot is trivial if and only if either p or q is equal to 1 or −1. The simplest nontrivial example is the (2,3)-torus knot, also known as the trefoil knot.
In knot theory, a branch of mathematics, a knot or link in the 3-dimensional sphere is called fibered or fibred if there is a 1-parameter family of Seifert surfaces for , where the parameter runs through the points of the unit circle , such that if is not equal to then the intersection of and is exactly .
In knot theory, a branch of topology, a Brunnian link is a nontrivial link that becomes a set of trivial unlinked circles if any one component is removed. In other words, cutting any loop frees all the other loops.
In mathematics, the Gordon–Luecke theorem on knot complements states that if the complements of two tame knots are homeomorphic, then the knots are equivalent. In particular, any homeomorphism between knot complements must take a meridian to a meridian.
In physical knot theory, each realization of a link or knot has an associated ropelength. Intuitively this is the minimal length of an ideally flexible rope that is needed to tie a given link, or knot. Knots and links that minimize ropelength are called ideal knots and ideal links respectively.
In molecular biology, the cerato-platanin family of proteins includes the phytotoxin cerato-platanin (CP) produced by the Ascomycete Ceratocystis platani. CP homologs are also found in both the Ascomycota and the Basidiomycota branches of Dikarya. This toxin causes the severe plant disease: canker stain. This protein occurs in the cell wall of the fungus and is involved in the host-pathogen interaction and induces both cell necrosis and phytoalexin synthesis which is one of the first plant defense-related events. CP, like other fungal surface proteins, is able to self-assemble in vitro. CP is a 120 amino acid protein, containing 40% hydrophobic residues. It is one of the rare examples of protein in which contains a Hopf link. The link is formed by covalent loops - the pieces of protein backbone closed by two disulphide bonds. The N-terminal region of CP is very similar to cerato-ulmin, a phytotoxic protein produced by the Ophiostoma species belonging to the hydrophobin family, which also self-assembles.
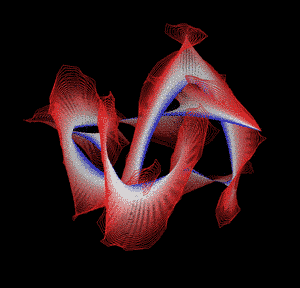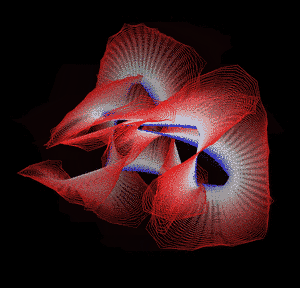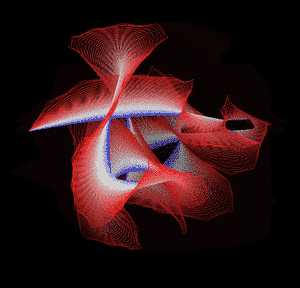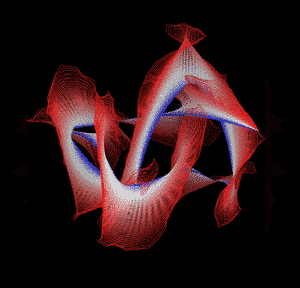
Knotted proteins are proteins whose backbones entangle themselves in a knot. One can imagine pulling a protein chain from both termini, as though pulling a string from both ends. When a knotted protein is “pulled” from both termini, it does not get disentangled. Knotted proteins are very rare, making up only about one percent of the proteins in the Protein Data Bank, and their folding mechanisms and function are not well understood. Although there are experimental and theoretical studies that hint to some answers, systematic answers to these questions have not yet been found.
In geometry, a quadrisecant or quadrisecant line of a space curve is a line that passes through four points of the curve. This is the largest possible number of intersections that a generic space curve can have with a line, and for such curves the quadrisecants form a discrete set of lines. Quadrisecants have been studied for curves of several types:
Complex lasso proteins are proteins in which a covalent loop is pierced by another piece of the backbone. Subclass of complex lasso proteins are Lasso peptides in which the loop is formed by post-translational amide bridge.
| Hyperbolic |
|
|---|---|
| Satellite | |
| Torus | |
| Invariants | |
| Notation and operations | |
| Other | |
