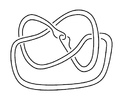
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself.
In mathematics, the JSJ decomposition, also known as the toral decomposition, is a topological construct given by the following theorem:
In mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface. Sometimes one considers only orientable Haken manifolds, in which case a Haken manifold is a compact, orientable, irreducible 3-manifold that contains an orientable, incompressible surface.

In knot theory, a prime knot or prime link is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite knots or composite links. It can be a nontrivial problem to determine whether a given knot is prime or not.

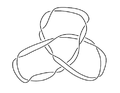
In knot theory, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining the two loose ends of a common overhand knot, resulting in a knotted loop. As the simplest knot, the trefoil is fundamental to the study of mathematical knot theory.

In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each. This construction plays a key role in the classification of closed surfaces.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.

In mathematics, a 3-manifold is a topological space that locally looks like a three-dimensional Euclidean space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small and close enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below.
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923. In 1969, John Conway showed a version of this polynomial, now called the Alexander–Conway polynomial, could be computed using a skein relation, although its significance was not realized until the discovery of the Jones polynomial in 1984. Soon after Conway's reworking of the Alexander polynomial, it was realized that a similar skein relation was exhibited in Alexander's paper on his polynomial.

Allen Edward Hatcher is an American topologist.

In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q are not coprime. A torus knot is trivial if and only if either p or q is equal to 1 or −1. The simplest nontrivial example is the (2,3)-torus knot, also known as the trefoil knot.

In mathematics, a Seifert surface is an orientable surface whose boundary is a given knot or link.
In mathematics, Alexander duality refers to a duality theory initiated by a result of J. W. Alexander in 1915, and subsequently further developed, particularly by Pavel Alexandrov and Lev Pontryagin. It applies to the homology theory properties of the complement of a subspace X in Euclidean space, a sphere, or other manifold. It is generalized by Spanier–Whitehead duality.
In the mathematical field of knot theory, the crosscap number of a knot K is the minimum of
In the mathematical field of knot theory, Fox n-coloring is a method of specifying a representation of a knot group or a group of a link onto the dihedral group of order n where n is an odd integer by coloring arcs in a link diagram. Ralph Fox discovered this method "in an effort to make the subject accessible to everyone" when he was explaining knot theory to undergraduate students at Haverford College in 1956. Fox n-coloring is an example of a conjugation quandle.
In the branch of mathematics called knot theory, the volume conjecture is an open problem that relates quantum invariants of knots to the hyperbolic geometry of their complements.
Horst Schubert was a German mathematician.