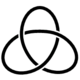
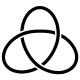
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself.

In the mathematical field of knot theory, a knot invariant is a quantity (in a broad sense) defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers (algebraic), but invariants can range from the simple, such as a yes/no answer, to those as complex as a homology theory (for example, "a knot invariant is a rule that assigns to any knot K a quantity φ(K) such that if K and K' are equivalent then φ(K) = φ(K')."). Research on invariants is not only motivated by the basic problem of distinguishing one knot from another but also to understand fundamental properties of knots and their relations to other branches of mathematics. Knot invariants are thus used in knot classification, both in "enumeration" and "duplication removal".
A knot invariant is a quantity defined on the set of all knots, which takes the same value for any two equivalent knots. For example, a knot group is a knot invariant.
Typically a knot invariant is a combinatorial quantity defined on knot diagrams. Thus if two knot diagrams differ with respect to some knot invariant, they must represent different knots. However, as is generally the case with topological invariants, if two knot diagrams share the same values with respect to a [single] knot invariant, then we still cannot conclude that the knots are the same.

In mathematics, a knot is an embedding of the circle into three-dimensional Euclidean space, R3. Often two knots are considered equivalent if they are ambient isotopic, that is, if there exists a continuous deformation of R3 which takes one knot to the other.

In knot theory, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining the two loose ends of a common overhand knot, resulting in a knotted loop. As the simplest knot, the trefoil is fundamental to the study of mathematical knot theory.
In the mathematical field of knot theory, the HOMFLY polynomial or HOMFLYPT polynomial, sometimes called the generalized Jones polynomial, is a 2-variable knot polynomial, i.e. a knot invariant in the form of a polynomial of variables m and l.
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.

In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. An object that is not chiral is said to be achiral.

In knot theory, a knot or link diagram is alternating if the crossings alternate under, over, under, over, as one travels along each component of the link. A link is alternating if it has an alternating diagram.

In the mathematical theory of knots, a pretzel link is a special kind of link. It consists of a finite number of tangles made of two intertwined circular helices. The tangles are connected cyclicly, and the first component of the first tangle is connected to the second component of the second tangle, the first component of the second tangle is connected to the second component of the third tangle, and so on. Finally, the first component of the last tangle is connected to the second component of the first. A pretzel link which is also a knot is a pretzel knot.

In mathematics, a Seifert surface is an orientable surface whose boundary is a given knot or link.
The Tait conjectures are three conjectures made by 19th-century mathematician Peter Guthrie Tait in his study of knots. The Tait conjectures involve concepts in knot theory such as alternating knots, chirality, and writhe. All of the Tait conjectures have been solved, the most recent being the Flyping conjecture.

A slice knot is a mathematical knot in 3-dimensional space that bounds an embedded disk in 4-dimensional space.

In knot theory, a Lissajous knot is a knot defined by parametric equations of the form
In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant. An invertible link is the link equivalent of an invertible knot.

Knots have been used for basic purposes such as recording information, fastening and tying objects together, for thousands of years. The early significant stimulus in knot theory would arrive later with Sir William Thomson and his vortex theory of the atom.

Ever since Sir William Thomson's vortex theory, mathematicians have tried to classify and tabulate all possible knots. As of May 2008, all prime knots up to 16 crossings have been tabulated. The major challenge of the process is that many apparently different knots may actually be different geometrical presentations of the same topological entity, and that proving or disproving knot equivalence is much more difficult than it at first seems.
In algebraic topology, a peripheral subgroup for a space-subspace pair X ⊃ Y is a certain subgroup of the fundamental group of the complementary space, π1(X − Y). Its conjugacy class is an invariant of the pair (X,Y). That is, any homeomorphism (X, Y) → (X′, Y′) induces an isomorphism π1(X − Y) → π1(X′ − Y′) taking peripheral subgroups to peripheral subgroups.
Gauss notation is a notation for mathematical knots. It is created by enumerating and classifying the crossings of an embedding of the knot in a plane. It is named after the German mathematician Carl Friedrich Gauss (1777–1855).
Mary Gertrude Haseman was an American mathematician known for her work in knot theory.