
In mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point O. An elliptic curve is defined over a field K and describes points in K2, the Cartesian product of K with itself. If the field's characteristic is different from 2 and 3, then the curve can be described as a plane algebraic curve which consists of solutions (x, y) for:
In mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on a closed interval [a, b] can be uniformly approximated as closely as desired by a polynomial function. Because polynomials are among the simplest functions, and because computers can directly evaluate polynomials, this theorem has both practical and theoretical relevance, especially in polynomial interpolation. The original version of this result was established by Karl Weierstrass in 1885 using the Weierstrass transform.
In the mathematical field of complex analysis, elliptic functions are special kinds of meromorphic functions, that satisfy two periodicity conditions. They are named elliptic functions because they come from elliptic integrals. Those integrals are in turn named elliptic because they first were encountered for the calculation of the arc length of an ellipse.

Karl Theodor Wilhelm Weierstrass was a German mathematician often cited as the "father of modern analysis". Despite leaving university without a degree, he studied mathematics and trained as a school teacher, eventually teaching mathematics, physics, botany and gymnastics. He later received an honorary doctorate and became professor of mathematics in Berlin.

Carl Gustav Jacob Jacobi was a German mathematician who made fundamental contributions to elliptic functions, dynamics, differential equations, determinants, and number theory.

Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of elliptic functions, differential equations, number theory, and to group theory. He is known for the famous determinantal identities, known as Frobenius–Stickelberger formulae, governing elliptic functions, and for developing the theory of biquadratic forms. He was also the first to introduce the notion of rational approximations of functions, and gave the first full proof for the Cayley–Hamilton theorem. He also lent his name to certain differential-geometric objects in modern mathematical physics, known as Frobenius manifolds.
In mathematics, the Weierstrass preparation theorem is a tool for dealing with analytic functions of several complex variables, at a given point P. It states that such a function is, up to multiplication by a function not zero at P, a polynomial in one fixed variable z, which is monic, and whose coefficients of lower degree terms are analytic functions in the remaining variables and zero at P.

In mathematics, the Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class of functions are also referred to as ℘-functions and they are usually denoted by the symbol ℘, a uniquely fancy script p. They play an important role in the theory of elliptic functions, i.e., meromorphic functions that are doubly periodic. A ℘-function together with its derivative can be used to parameterize elliptic curves and they generate the field of elliptic functions with respect to a given period lattice.
In number theory and algebraic geometry, a modular curveY(Γ) is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL(2, Z). The term modular curve can also be used to refer to the compactified modular curvesX(Γ) which are compactifications obtained by adding finitely many points to this quotient. The points of a modular curve parametrize isomorphism classes of elliptic curves, together with some additional structure depending on the group Γ. This interpretation allows one to give a purely algebraic definition of modular curves, without reference to complex numbers, and, moreover, prove that modular curves are defined either over the field of rational numbers Q or a cyclotomic field Q(ζn). The latter fact and its generalizations are of fundamental importance in number theory.

Sergei Natanovich Bernstein was a Ukrainian and Russian mathematician of Jewish origin known for contributions to partial differential equations, differential geometry, probability theory, and approximation theory.
In mathematics, the Weierstrass functions are special functions of a complex variable that are auxiliary to the Weierstrass elliptic function. They are named for Karl Weierstrass. The relation between the sigma, zeta, and functions is analogous to that between the sine, cotangent, and squared cosecant functions: the logarithmic derivative of the sine is the cotangent, whose derivative is negative the squared cosecant.

In mathematics, the Weierstrass–Enneper parameterization of minimal surfaces is a classical piece of differential geometry.
Alfred Enneper was a German mathematician. Enneper earned his PhD from the Georg-August-Universität Göttingen in 1856, under the supervision of Peter Gustav Lejeune Dirichlet, for his dissertation about functions with complex arguments. After his habilitation in 1859 in Göttingen, he was from 1870 on Professor (Extraordinarius) at Göttingen.
In mathematics, a doubly periodic function is a function defined on the complex plane and having two "periods", which are complex numbers u and v that are linearly independent as vectors over the field of real numbers. That u and v are periods of a function ƒ means that

In differential geometry and algebraic geometry, the Enneper surface is a self-intersecting surface that can be described parametrically by:
In Riemannian geometry, a Bryant surface is a 2-dimensional surface embedded in 3-dimensional hyperbolic space with constant mean curvature equal to 1. These surfaces take their name from the geometer Robert Bryant, who proved that every simply-connected minimal surface in 3-dimensional Euclidean space is isometric to a Bryant surface by a holomorphic parameterization analogous to the (Euclidean) Weierstrass–Enneper parameterization.
This is a timeline of the theory of abelian varieties in algebraic geometry, including elliptic curves.

In mathematics, Bour's minimal surface is a two-dimensional minimal surface, embedded with self-crossings into three-dimensional Euclidean space. It is named after Edmond Bour, whose work on minimal surfaces won him the 1861 mathematics prize of the French Academy of Sciences.
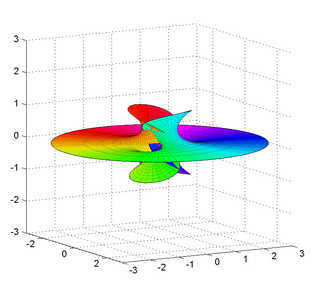
In differential geometry, a Richmond surface is a minimal surface first described by Herbert William Richmond in 1904. It is a family of surfaces with one planar end and one Enneper surface-like self-intersecting end.