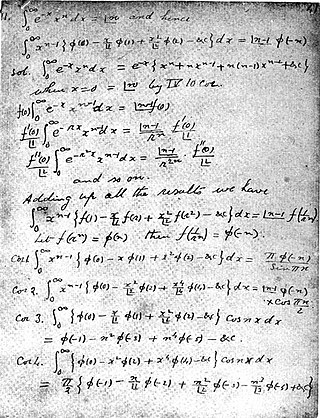Weierstrass preparation theorem

Last updated March 08, 2024

In mathematics, the Weierstrass preparation theorem is a tool for dealing with analytic functions of several complex variables, at a given point P. It states that such a function is, up to multiplication by a function not zero at P, a polynomial in one fixed variable z, which is monic, and whose coefficients of lower degree terms are analytic functions in the remaining variables and zero at P.

There are also a number of variants of the theorem, that extend the idea of factorization in some ring R as u·w, where u is a unit and w is some sort of distinguished Weierstrass polynomial. Carl Siegel has disputed the attribution of the theorem to Weierstrass, saying that it occurred under the current name in some of late nineteenth century Traités d'analyse without justification.

Complex analytic functions

For one variable, the local form of an analytic function f(z) near 0 is z^kh(z) where h(0) is not 0, and k is the order of the zero of f at 0. This is the result that the preparation theorem generalises. We pick out one variable z, which we may assume is first, and write our complex variables as (z, z₂, ..., z_n). A Weierstrass polynomial W(z) is

z^k + g_k−1z^k−1 + ... + g₀

where g_i(z₂, ..., z_n) is analytic and g_i(0, ..., 0) = 0.

Then the theorem states that for analytic functions f, if

f(0, ...,0) = 0,

and

f(z, z₂, ..., z_n)

as a power series has some term only involving z, we can write (locally near (0, ..., 0))

f(z, z₂, ..., z_n) = W(z)h(z, z₂, ..., z_n)

with h analytic and h(0, ..., 0) not 0, and W a Weierstrass polynomial.

This has the immediate consequence that the set of zeros of f, near (0, ..., 0), can be found by fixing any small values of z₂, ..., z_n and then solving the equation W(z)=0. The corresponding values of z form a number of continuously-varying branches, in number equal to the degree of W in z. In particular f cannot have an isolated zero.

Division theorem

A related result is the Weierstrass division theorem, which states that if f and g are analytic functions, and g is a Weierstrass polynomial of degree N, then there exists a unique pair h and j such that f = gh + j, where j is a polynomial of degree less than N. In fact, many authors prove the Weierstrass preparation as a corollary of the division theorem. It is also possible to prove the division theorem from the preparation theorem so that the two theorems are actually equivalent.^[1]

Applications

The Weierstrass preparation theorem can be used to show that the ring of germs of analytic functions in n variables is a Noetherian ring, which is also referred to as the Rückert basis theorem.^[2]

Smooth functions

There is a deeper preparation theorem for smooth functions, due to Bernard Malgrange, called the Malgrange preparation theorem. It also has an associated division theorem, named after John Mather.

Formal power series in complete local rings

There is an analogous result, also referred to as the Weierstrass preparation theorem, for the ring of formal power series over complete local rings A:^[3] for any power series $f=\sum _{n=0}^{\infty }a_{n}t^{n}\in A[[t]]$ such that not all $a_{n}$ are in the maximal ideal ${\mathfrak {m}}$ of A, there is a unique unit u in $A[[t]]$ and a polynomial F of the form $F=t^{s}+b_{s-1}t^{s-1}+\dots +b_{0}$ with $b_{i}\in {\mathfrak {m}}$ (a so-called distinguished polynomial) such that

f=uF.

Since $A[[t]]$ is again a complete local ring, the result can be iterated and therefore gives similar factorization results for formal power series in several variables.

For example, this applies to the ring of integers in a p-adic field. In this case the theorem says that a power series f(z) can always be uniquely factored as πⁿ·u(z)·p(z), where u(z) is a unit in the ring of power series, p(z) is a distinguished polynomial (monic, with the coefficients of the non-leading terms each in the maximal ideal), and π is a fixed uniformizer.

An application of the Weierstrass preparation and division theorem for the ring $\mathbf {Z} _{p}[[t]]$ (also called Iwasawa algebra) occurs in Iwasawa theory in the description of finitely generated modules over this ring.^[4]

There exists a non-commutative version of Weierstrass division and preparation, with A being a not necessarily commutative ring, and with formal skew power series in place of formal power series.^[5]

Tate algebras

There is also a Weierstrass preparation theorem for Tate algebras

T_{n}(k)=\left\{\sum _{\nu _{1},\dots ,\nu _{n}\geq 0}a_{\nu _{1},\dots ,\nu _{n}}X_{1}^{\nu _{1}}\cdots X_{n}^{\nu _{n}},|a_{\nu _{1},\dots ,\nu _{n}}|\to 0{\text{ for }}\nu _{1}+\dots +\nu _{n}\to \infty \right\}

over a complete non-archimedean field k.^[6] These algebras are the basic building blocks of rigid geometry. One application of this form of the Weierstrass preparation theorem is the fact that the rings $T_{n}(k)$ are Noetherian.

Related Research Articles

In mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on a closed interval $[a, b]$ can be uniformly approximated as closely as desired by a polynomial function. Because polynomials are among the simplest functions, and because computers can directly evaluate polynomials, this theorem has both practical and theoretical relevance, especially in polynomial interpolation. The original version of this result was established by Karl Weierstrass in 1885 using the Weierstrass transform.

In mathematics, a transcendental number is a real or complex number that is not algebraic – that is, not the root of a non-zero polynomial of finite degree with rational coefficients. The best-known transcendental numbers are $π$ and $e$ .

The fundamental theorem of algebra, also called d'Alembert's theorem or the d'Alembert–Gauss theorem, states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This includes polynomials with real coefficients, since every real number is a complex number with its imaginary part equal to zero.

In mathematics, a unique factorization domain (UFD) is a ring in which a statement analogous to the fundamental theorem of arithmetic holds. Specifically, a UFD is an integral domain in which every non-zero non-unit element can be written as a product of irreducible elements, uniquely up to order and units.

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex analytic functions exhibit properties that do not generally hold for real analytic functions. A function is analytic if and only if its Taylor series about $converges to the function in some neighborhood for every in its domain. It is important to note that it is a neighborhood and not just at some point, since every differentiable function has at least a tangent line at every point, which is its Taylor series of order 1. So just having a polynomial expansion at singular points is not enough, and the Taylor series must also converge to the function on points adjacent to to be considered an analytic function. As a counterexample see the Weierstrass function or the Fabius function.$

In mathematics, Hilbert's Nullstellensatz is a theorem that establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields. This relationship was discovered by David Hilbert, who proved the Nullstellensatz in his second major paper on invariant theory in 1893.

<span class="mw-page-title-main">Root of unity</span> Number that has an integer power equal to 1

In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that yields 1 when raised to some positive integer power $n$ . Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.

The Riemann–Roch theorem is an important theorem in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeros and allowed poles. It relates the complex analysis of a connected compact Riemann surface with the surface's purely topological genus g, in a way that can be carried over into purely algebraic settings.

In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation $h (x, y, t) = 0$ can be restricted to the affine algebraic plane curve of equation $h (x, y, 1) = 0$ . These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.

In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation that accepts a function and returns another function.

In algebraic geometry, a projective variety over an algebraically closed field k is a subset of some projective n-space $over k that is the zero-locus of some finite family of homogeneous polynomials of n + 1 variables with coefficients in k, that generate a prime ideal, the defining ideal of the variety. Equivalently, an algebraic variety is projective if it can be embedded as a Zariski closed subvariety of .$

In transcendental number theory, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states the following:

The theory of functions of several complex variables is the branch of mathematics dealing with functions defined on the complex coordinate space $, that is, n -tuples of complex numbers. The name of the field dealing with the properties of these functions is called several complex variables, which the Mathematics Subject Classification has as a top-level heading.$

In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates with coefficients in another ring, often a field.

In mathematics, complex multiplication (CM) is the theory of elliptic curves E that have an endomorphism ring larger than the integers. Put another way, it contains the theory of elliptic functions with extra symmetries, such as are visible when the period lattice is the Gaussian integer lattice or Eisenstein integer lattice.

In abstract algebra, a discrete valuation ring (DVR) is a principal ideal domain (PID) with exactly one non-zero maximal ideal.

In mathematics, Hölder's theorem states that the gamma function does not satisfy any algebraic differential equation whose coefficients are rational functions. This result was first proved by Otto Hölder in 1887; several alternative proofs have subsequently been found.

In mathematics, the Iwasawa algebra Λ(G) of a profinite group G is a variation of the group ring of G with p-adic coefficients that take the topology of G into account. More precisely, Λ(G) is the inverse limit of the group rings Z_p(G/H) as H runs through the open normal subgroups of G. Commutative Iwasawa algebras were introduced by Iwasawa (1959) in his study of Z_p extensions in Iwasawa theory, and non-commutative Iwasawa algebras of compact p-adic analytic groups were introduced by Lazard (1965).

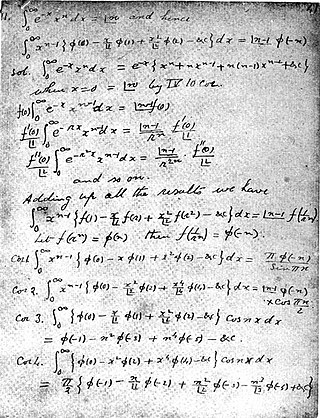
In mathematics, Ramanujan's Master Theorem, named after Srinivasa Ramanujan, is a technique that provides an analytic expression for the Mellin transform of an analytic function.

In algebra, the ring of restricted power series is the subring of a formal power series ring that consists of power series whose coefficients approach zero as degree goes to infinity. Over a non-archimedean complete field, the ring is also called a Tate algebra. Quotient rings of the ring are used in the study of a formal algebraic space as well as rigid analysis, the latter over non-archimedean complete fields.

References

↑ Grauert, Hans; Remmert, Reinhold (1971), Analytische Stellenalgebren (in German), Springer, p. 43, doi:10.1007/978-3-642-65033-8, ISBN 978-3-642-65034-5
↑ Ebeling, Wolfgang (2007), Functions of Several Complex Variables and Their Singularities, Proposition 2.19: American Mathematical Society {{citation}}: CS1 maint: location (link)
↑ Nicolas Bourbaki (1972), Commutative algebra, chapter VII, §3, no. 9, Proposition 6: Hermann{{citation}}: CS1 maint: location (link)
↑ Lawrence Washington (1982), Introduction to cyclotomic fields, Theorem 13.12: Springer{{citation}}: CS1 maint: location (link)
↑ Otmar Venjakob (2003). "A noncommutative Weierstrass preparation theorem and applications to Iwasawa theory". J. Reine Angew. Math. 2003 (559): 153–191. arXiv: math/0204358 . doi:10.1515/crll.2003.047. S2CID 14265629 . Retrieved 2022-01-27. Theorem 3.1, Corollary 3.2
↑ Bosch, Siegfried; Güntzer, Ulrich; Remmert, Reinhold (1984), Non-archimedean analysis, Chapters 5.2.1, 5.2.2: Springer{{citation}}: CS1 maint: location (link)

Lewis, Andrew, Notes on Global Analysis
Siegel, C. L. (1969), "Zu den Beweisen des Vorbereitungssatzes von Weierstrass", Number Theory and Analysis (Papers in Honor of Edmund Landau), New York: Plenum, pp. 297–306, MR 0268402 , reprinted in Siegel, Carl Ludwig (1979), Chandrasekharan, K.; Maass., H. (eds.), Gesammelte Abhandlungen. Band IV, Berlin-New York: Springer-Verlag, pp. 1–8, ISBN 0-387-09374-5, MR 0543842
Solomentsev, E.D. (2001) [1994], "Weierstrass theorem", Encyclopedia of Mathematics , EMS Press
Stickelberger, L. (1887), "Ueber einen Satz des Herrn Noether", Mathematische Annalen, 30 (3): 401–409, doi:10.1007/BF01443952, S2CID 121360367
Weierstrass, K. (1895), Mathematische Werke. II. Abhandlungen 2, Berlin: Mayer & Müller, pp. 135–142 reprinted by Johnson, New York, 1967.

External links

Lebl, Jiří (6 July 2021). "Weierstrass Preparation and Division Theorems. (2021, September 5)". LibreTexts.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Grauert, Hans; Remmert, Reinhold (1971), Analytische Stellenalgebren (in German), Springer, p. 43, doi:10.1007/978-3-642-65033-8, ISBN 978-3-642-65034-5

[2] Ebeling, Wolfgang (2007), Functions of Several Complex Variables and Their Singularities, Proposition 2.19: American Mathematical Society {{citation}}: CS1 maint: location (link)

[3] Nicolas Bourbaki (1972), Commutative algebra, chapter VII, §3, no. 9, Proposition 6: Hermann{{citation}}: CS1 maint: location (link)

[4] Lawrence Washington (1982), Introduction to cyclotomic fields, Theorem 13.12: Springer{{citation}}: CS1 maint: location (link)

[5] Otmar Venjakob (2003). "A noncommutative Weierstrass preparation theorem and applications to Iwasawa theory". J. Reine Angew. Math. 2003 (559): 153–191. arXiv: math/0204358 . doi:10.1515/crll.2003.047. S2CID 14265629 . Retrieved 2022-01-27. Theorem 3.1, Corollary 3.2

[6] Bosch, Siegfried; Güntzer, Ulrich; Remmert, Reinhold (1984), Non-archimedean analysis, Chapters 5.2.1, 5.2.2: Springer{{citation}}: CS1 maint: location (link)

[1]

[2]

[3]

[4]

[5]

[6]