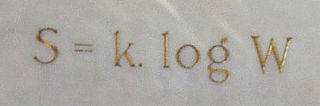Entropy is a scientific concept that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication.
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in the fields of physics, biology, chemistry, neuroscience, computer science, information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion.

Thermodynamics deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of thermodynamics, which convey a quantitative description using measurable macroscopic physical quantities, but may be explained in terms of microscopic constituents by statistical mechanics. Thermodynamics plays a role in a wide variety of topics in science and engineering.

The second law of thermodynamics is a physical law based on universal empirical observation concerning heat and energy interconversions. A simple statement of the law is that heat always flows spontaneously from hotter to colder regions of matter. Another statement is: "Not all heat can be converted into work in a cyclic process."

In physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons. As the study of the statistical mechanics of black-body radiation led to the development of the theory of quantum mechanics, the effort to understand the statistical mechanics of black holes has had a deep impact upon the understanding of quantum gravity, leading to the formulation of the holographic principle.

Ludwig Eduard Boltzmann was an Austrian physicist and philosopher. His greatest achievements were the development of statistical mechanics, and the statistical explanation of the second law of thermodynamics. In 1877 he provided the current definition of entropy, , where Ω is the number of microstates whose energy equals the system's energy, interpreted as a measure of the statistical disorder of a system. Max Planck named the constant kB the Boltzmann constant.

In science, a process that is not reversible is called irreversible. This concept arises frequently in thermodynamics. All complex natural processes are irreversible, although a phase transition at the coexistence temperature is well approximated as reversible.

The laws of thermodynamics are a set of scientific laws which define a group of physical quantities, such as temperature, energy, and entropy, that characterize thermodynamic systems in thermodynamic equilibrium. The laws also use various parameters for thermodynamic processes, such as thermodynamic work and heat, and establish relationships between them. They state empirical facts that form a basis of precluding the possibility of certain phenomena, such as perpetual motion. In addition to their use in thermodynamics, they are important fundamental laws of physics in general and are applicable in other natural sciences.

In statistical thermodynamics, thermodynamic beta, also known as coldness, is the reciprocal of the thermodynamic temperature of a system:.
In physics, maximum entropy thermodynamics views equilibrium thermodynamics and statistical mechanics as inference processes. More specifically, MaxEnt applies inference techniques rooted in Shannon information theory, Bayesian probability, and the principle of maximum entropy. These techniques are relevant to any situation requiring prediction from incomplete or insufficient data. MaxEnt thermodynamics began with two papers by Edwin T. Jaynes published in the 1957 Physical Review.

In statistical mechanics, a microstate is a specific configuration of a system that describes the precise positions and momenta of all the individual particles or components that make up the system. Each microstate has a certain probability of occurring during the course of the system's thermal fluctuations.
The mathematical expressions for thermodynamic entropy in the statistical thermodynamics formulation established by Ludwig Boltzmann and J. Willard Gibbs in the 1870s are similar to the information entropy by Claude Shannon and Ralph Hartley, developed in the 1940s.

The maximum power principle or Lotka's principle has been proposed as the fourth principle of energetics in open system thermodynamics. According to American ecologist Howard T. Odum, "The maximum power principle can be stated: During self-organization, system designs develop and prevail that maximize power intake, energy transformation, and those uses that reinforce production and efficiency."
The concept entropy was first developed by German physicist Rudolf Clausius in the mid-nineteenth century as a thermodynamic property that predicts that certain spontaneous processes are irreversible or impossible. In statistical mechanics, entropy is formulated as a statistical property using probability theory. The statistical entropy perspective was introduced in 1870 by Austrian physicist Ludwig Boltzmann, who established a new field of physics that provided the descriptive linkage between the macroscopic observation of nature and the microscopic view based on the rigorous treatment of large ensembles of microscopic states that constitute thermodynamic systems.
In thermodynamics, the interpretation of entropy as a measure of energy dispersal has been exercised against the background of the traditional view, introduced by Ludwig Boltzmann, of entropy as a quantitative measure of disorder. The energy dispersal approach avoids the ambiguous term 'disorder'. An early advocate of the energy dispersal conception was Edward A. Guggenheim in 1949, using the word 'spread'.

In thermodynamics, entropy is a numerical quantity that shows that many physical processes can go in only one direction in time. For example, cream and coffee can be mixed together, but cannot be "unmixed"; a piece of wood can be burned, but cannot be "unburned". The word 'entropy' has entered popular usage to refer to a lack of order or predictability, or of a gradual decline into disorder. A more physical interpretation of thermodynamic entropy refers to spread of energy or matter, or to extent and diversity of microscopic motion.

In thermodynamics, entropy is often associated with the amount of order or disorder in a thermodynamic system. This stems from Rudolf Clausius' 1862 assertion that any thermodynamic process always "admits to being reduced [reduction] to the alteration in some way or another of the arrangement of the constituent parts of the working body" and that internal work associated with these alterations is quantified energetically by a measure of "entropy" change, according to the following differential expression:
Research concerning the relationship between the thermodynamic quantity entropy and both the origin and evolution of life began around the turn of the 20th century. In 1910 American historian Henry Adams printed and distributed to university libraries and history professors the small volume A Letter to American Teachers of History proposing a theory of history based on the second law of thermodynamics and on the principle of entropy.
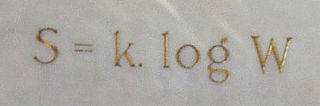
In statistical mechanics, Boltzmann's equation is a probability equation relating the entropy , also written as , of an ideal gas to the multiplicity, the number of real microstates corresponding to the gas's macrostate:

Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making up a substance.