
A covalent bond is a chemical bond that involves the sharing of electrons to form electron pairs between atoms. These electron pairs are known as shared pairs or bonding pairs. The stable balance of attractive and repulsive forces between atoms, when they share electrons, is known as covalent bonding. For many molecules, the sharing of electrons allows each atom to attain the equivalent of a full valence shell, corresponding to a stable electronic configuration. In organic chemistry, covalent bonding is much more common than ionic bonding.
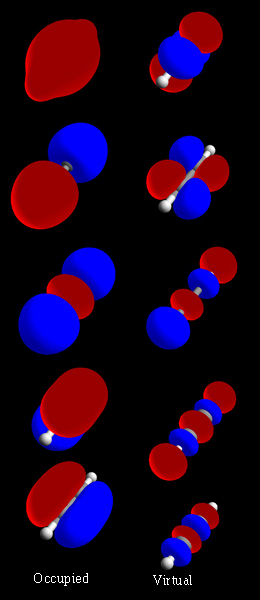
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The terms atomic orbital and molecular orbital were introduced by Robert S. Mulliken in 1932 to mean one-electron orbital wave functions. At an elementary level, they are used to describe the region of space in which a function has a significant amplitude.

In theoretical chemistry, a conjugated system is a system of connected p-orbitals with delocalized electrons in a molecule, which in general lowers the overall energy of the molecule and increases stability. It is conventionally represented as having alternating single and multiple bonds. Lone pairs, radicals or carbenium ions may be part of the system, which may be cyclic, acyclic, linear or mixed. The term "conjugated" was coined in 1899 by the German chemist Johannes Thiele.
Coupled cluster (CC) is a numerical technique used for describing many-body systems. Its most common use is as one of several post-Hartree–Fock ab initio quantum chemistry methods in the field of computational chemistry, but it is also used in nuclear physics. Coupled cluster essentially takes the basic Hartree–Fock molecular orbital method and constructs multi-electron wavefunctions using the exponential cluster operator to account for electron correlation. Some of the most accurate calculations for small to medium-sized molecules use this method.
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state.
In chemistry, molecular orbital theory is a method for describing the electronic structure of molecules using quantum mechanics. It was proposed early in the 20th century.
Møller–Plesset perturbation theory (MP) is one of several quantum chemistry post-Hartree–Fock ab initio methods in the field of computational chemistry. It improves on the Hartree–Fock method by adding electron correlation effects by means of Rayleigh–Schrödinger perturbation theory (RS-PT), usually to second (MP2), third (MP3) or fourth (MP4) order. Its main idea was published as early as 1934 by Christian Møller and Milton S. Plesset.
Modern valence bond theory is the application of valence bond theory (VBT) with computer programs that are competitive in accuracy and economy with programs for the Hartree–Fock or post-Hartree-Fock methods. The latter methods dominated quantum chemistry from the advent of digital computers because they were easier to program. The early popularity of valence bond methods thus declined. It is only recently that the programming of valence bond methods has improved. These developments are due to and described by Gerratt, Cooper, Karadakov and Raimondi (1997); Li and McWeeny (2002); Joop H. van Lenthe and co-workers (2002); Song, Mo, Zhang and Wu (2005); and Shaik and Hiberty (2004)
In solid-state physics, the tight-binding model is an approach to the calculation of electronic band structure using an approximate set of wave functions based upon superposition of wave functions for isolated atoms located at each atomic site. The method is closely related to the LCAO method used in chemistry. Tight-binding models are applied to a wide variety of solids. The model gives good qualitative results in many cases and can be combined with other models that give better results where the tight-binding model fails. Though the tight-binding model is a one-electron model, the model also provides a basis for more advanced calculations like the calculation of surface states and application to various kinds of many-body problem and quasiparticle calculations.
The Hückel method or Hückel molecular orbital theory, proposed by Erich Hückel in 1930, is a simple method for calculating molecular orbitals as linear combinations of atomic orbitals. The theory predicts the molecular orbitals for π-electrons in π-delocalized molecules, such as ethylene, benzene, butadiene, and pyridine. It provides the theoretical basis for Hückel's rule that cyclic, planar molecules or ions with π-electrons are aromatic. It was later extended to conjugated molecules such as pyridine, pyrrole and furan that contain atoms other than carbon and hydrogen (heteroatoms). A more dramatic extension of the method to include σ-electrons, known as the extended Hückel method (EHM), was developed by Roald Hoffmann. The extended Hückel method gives some degree of quantitative accuracy for organic molecules in general and was used to provide computational justification for the Woodward–Hoffmann rules. To distinguish the original approach from Hoffmann's extension, the Hückel method is also known as the simple Hückel method (SHM).
Zero differential overlap is an approximation in computational molecular orbital theory that is the central technique of semi-empirical methods in quantum chemistry. When computers were first used to calculate bonding in molecules, it was only possible to calculate diatomic molecules. As computers advanced, it became possible to study larger molecules, but the use of this approximation has always allowed the study of even larger molecules. Currently semi-empirical methods can be applied to molecules as large as whole proteins. The approximation involves ignoring certain integrals, usually two-electron repulsion integrals. If the number of orbitals used in the calculation is N, the number of two-electron repulsion integrals scales as N4. After the approximation is applied the number of such integrals scales as N2, a much smaller number, simplifying the calculation.
In chemistry and physics, the exchange interaction or exchange force is a quantum mechanical effect that only occurs between identical particles.
A molecular orbital diagram, or MO diagram, is a qualitative descriptive tool explaining chemical bonding in molecules in terms of molecular orbital theory in general and the linear combination of atomic orbitals (LCAO) method in particular. A fundamental principle of these theories is that as atoms bond to form molecules, a certain number of atomic orbitals combine to form the same number of molecular orbitals, although the electrons involved may be redistributed among the orbitals. This tool is very well suited for simple diatomic molecules such as dihydrogen, dioxygen, and carbon monoxide but becomes more complex when discussing even comparatively simple polyatomic molecules, such as methane. MO diagrams can explain why some molecules exist and others do not. They can also predict bond strength, as well as the electronic transitions that can take place.
Within computational chemistry, the Slater–Condon rules express integrals of one- and two-body operators over wavefunctions constructed as Slater determinants of orthonormal orbitals in terms of the individual orbitals. In doing so, the original integrals involving N-electron wavefunctions are reduced to sums over integrals involving at most two molecular orbitals, or in other words, the original 3N dimensional integral is expressed in terms of many three- and six-dimensional integrals.
In quantum chemistry, a natural bond orbital or NBO is a calculated bonding orbital with maximum electron density. The NBOs are one of a sequence of natural localized orbital sets that include "natural atomic orbitals" (NAO), "natural hybrid orbitals" (NHO), "natural bonding orbitals" (NBO) and "natural (semi-)localized molecular orbitals" (NLMO). These natural localized sets are intermediate between basis atomic orbitals (AO) and molecular orbitals (MO):
In physics, the total position-spread (TPS) tensor is a quantity originally introduced in the modern theory of electrical conductivity. In the case of molecular systems, this tensor measures the fluctuation of the electrons around their mean positions, which corresponds to the delocalization of the electronic charge within a molecular system. The total position-spread can discriminate between metals and insulators taking information from the ground state wave function. This quantity can be very useful as an indicator to characterize Intervalence charge transfer processes, the bond nature of molecules, and Metal–insulator transition.
In theoretical chemistry, the bonding orbital is used in molecular orbital (MO) theory to describe the attractive interactions between the atomic orbitals of two or more atoms in a molecule. In MO theory, electrons are portrayed to move in waves. When more than one of these waves come close together, the in-phase combination of these waves produces an interaction that leads to a species that is greatly stabilized. The result of the waves’ constructive interference causes the density of the electrons to be found within the binding region, creating a stable bond between the two species.
In modern valence bond (VB) theory calculations, Chirgwin–Coulson weights are the relative weights of a set of possible VB structures of a molecule. Related methods of finding the relative weights of valence bond structures are the Löwdin and the inverse weights.
Intrinsic bond orbitals (IBO) are localized molecular orbitals giving exact and non-empirical representations of wave functions. They are obtained by unitary transformation and form an orthogonal set of orbitals localized on a minimal number of atoms. IBOs present an intuitive and unbiased interpretation of chemical bonding with naturally arising Lewis structures. For this reason IBOs have been successfully employed for the elucidation of molecular structures and electron flow along the intrinsic reaction coordinate (IRC). IBOs have also found application as Wannier functions in the study of solids.
Oxidation state localized orbitals (OSLOs) is a new concept used to determine the oxidation states of each fragment for the coordination complexes. Based on the result of density functional theory (DFT), all the occupied molecular orbitals are remixed to get the oxidation state localized orbitals. These orbitals are assigned to one of the fragments in this molecule based on the fragment orbital localization index (FOLI). After all the electrons are assigned, the oxidation states of each fragment could be obtained by calculating the difference between the number of electrons and protons in each fragment.














