Logarithmically concave measure

Last updated

In mathematics, a Borel measure μ on n-dimensional Euclidean space is called logarithmically concave (or log-concave for short) if, for any compact subsets A and B of and 0 < λ < 1, one has

Mathematics Field of study concerning quantity, patterns and change

Mathematics includes the study of such topics as quantity, structure, space, and change.

In mathematics, specifically in measure theory, a Borel measure on a topological space is a measure that is defined on all open sets. Some authors require additional restrictions on the measure, as described below.

Dimension Maximum number of independent directions within a mathematical space

In physics and mathematics, the dimension of a mathematical space is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it – for example, the point at 5 on a number line. A surface such as a plane or the surface of a cylinder or sphere has a dimension of two because two coordinates are needed to specify a point on it – for example, both a latitude and longitude are required to locate a point on the surface of a sphere. The inside of a cube, a cylinder or a sphere is three-dimensional because three coordinates are needed to locate a point within these spaces.

Contents

where λ A + (1 − λ) B denotes the Minkowski sum of λ A and (1 − λ) B. [1]

Examples

The Brunn–Minkowski inequality asserts that the Lebesgue measure is log-concave. The restriction of the Lebesgue measure to any convex set is also log-concave.

In mathematics, the Brunn–Minkowski theorem is an inequality relating the volumes of compact subsets of Euclidean space. The original version of the Brunn–Minkowski theorem applied to convex sets; the generalization to compact nonconvex sets stated here is due to Lazar Lyusternik (1935).

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called n-dimensional volume, n-volume, or simply volume. It is used throughout real analysis, in particular to define Lebesgue integration. Sets that can be assigned a Lebesgue measure are called Lebesgue-measurable; the measure of the Lebesgue-measurable set A is here denoted by λ(A).

Convex set In geometry, set that intersects every line into a line segment

In geometry, a convex set or a convex region is a subset of a Euclidean space, or more generally an affine space over the reals, that intersects every line into a line segment. Equivalently, this is a subset that is closed under convex combinations. For example, a solid cube is a convex set, but anything that is hollow or has an indent, for example, a crescent shape, is not convex.

By a theorem of Borell, [2] a measure is log-concave if and only if it has a density with respect to the Lebesgue measure on some affine hyperplane, and this density is a logarithmically concave function. Thus, any Gaussian measure is log-concave.

In convex analysis, a non-negative function f : Rn → R+ is logarithmically concave if its domain is a convex set, and if it satisfies the inequality

In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces. Gaussian measures are named after the German mathematician Carl Friedrich Gauss. One reason why Gaussian measures are so ubiquitous in probability theory is the Central Limit Theorem. Loosely speaking, it states that if a random variable X is obtained by summing a large number N of independent random variables of order 1, then X is of order and its law is approximately Gaussian.

The Prékopa–Leindler inequality shows that a convolution of log-concave measures is log-concave.

In mathematics, the Prékopa–Leindler inequality is an integral inequality closely related to the reverse Young's inequality, the Brunn–Minkowski inequality and a number of other important and classical inequalities in analysis. The result is named after the Hungarian mathematicians András Prékopa and László Leindler.

Convolution mathematical operation

In mathematics convolution is a mathematical operation on two functions to produce a third function that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, it differs from cross-correlation only in that either f (x) or g(x) is reflected about the y-axis; thus it is a cross-correlation of f (x) and g(−x), or f (−x) and g(x). For continuous functions, the cross-correlation operator is the adjoint of the convolution operator.

See also

In measure and probability theory in mathematics, a convex measure is a probability measure that — loosely put — does not assign more mass to any intermediate set “between” two measurable sets A and B than it does to A or B individually. There are multiple ways in which the comparison between the probabilities of A and B and the intermediate set can be made, leading to multiple definitions of convexity, such as log-concavity, harmonic convexity, and so on. The mathematician Christer Borell was a pioneer of the detailed study of convex measures on locally convex spaces in the 1970s.

Related Research Articles

In mathematical analysis, a null set is a set that can be covered by a countable union of intervals of arbitrarily small total length. The notion of null set in set theory anticipates the development of Lebesgue measure since a null set necessarily has measure zero. More generally, on a given measure space a null set is a set such that .

In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue, although according to the Bourbaki group they were first introduced by Frigyes Riesz. Lp spaces form an important class of Banach spaces in functional analysis, and of topological vector spaces. Because of their key role in the mathematical analysis of measure and probability spaces, Lebesgue spaces are used also in the theoretical discussion of problems in physics, statistics, finance, engineering, and other disciplines.

In calculus, absolute continuity is a smoothness property of functions that is stronger than continuity and uniform continuity. The notion of absolute continuity allows one to obtain generalizations of the relationship between the two central operations of calculus—differentiation and integration. This relationship is commonly characterized in the framework of Riemann integration, but with absolute continuity it may be formulated in terms of Lebesgue integration. For real-valued functions on the real line, two interrelated notions appear: absolute continuity of functions and absolute continuity of measures. These two notions are generalized in different directions. The usual derivative of a function is related to the Radon–Nikodym derivative, or density, of a measure.

Jensens inequality Theorem of convex functions

In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proven by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context, some of which are presented below. In its simplest form the inequality states that the convex transformation of a mean is less than or equal to the mean applied after convex transformation; it is a simple corollary that the opposite is true of concave transformations.

In mathematics, the isoperimetric inequality is a geometric inequality involving the surface area of a set and its volume. In -dimensional space the inequality lower bounds the surface area of a set by its volume ,

Minkowski addition

In geometry, the Minkowski sum of two sets of position vectors A and B in Euclidean space is formed by adding each vector in A to each vector in B, i.e., the set

Quantum statistical mechanics is statistical mechanics applied to quantum mechanical systems. In quantum mechanics a statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be shown under various mathematical formalisms for quantum mechanics. One such formalism is provided by quantum logic.

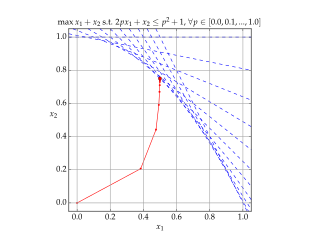
Interior-point method

Interior-point methods are a certain class of algorithms that solve linear and nonlinear convex optimization problems.

In mathematics, two positive measures μ and ν defined on a measurable space are called singular if there exist two disjoint sets A and B in Σ whose union is Ω such that μ is zero on all measurable subsets of B while ν is zero on all measurable subsets of A. This is denoted by

In mathematics, the Minkowski–Steiner formula is a formula relating the surface area and volume of compact subsets of Euclidean space. More precisely, it defines the surface area as the "derivative" of enclosed volume in an appropriate sense.

In mathematics, the Borell–Brascamp–Lieb inequality is an integral inequality due to many different mathematicians but named after Christer Borell, Herm Jan Brascamp and Elliott Lieb.

In mathematics, geometric measure theory (GMT) is the study of geometric properties of sets through measure theory. It allows mathematicians to extend tools from differential geometry to a much larger class of surfaces that are not necessarily smooth.

Carathéodory's criterion is a result in measure theory that was formulated by Greek mathematician Constantin Carathéodory. Its statement is as follows: Let denote the Lebesgue outer measure on , and let . Then is Lebesgue measurable if and only if for every . Notice that is not required to be a measurable set.

In mathematics, the Fortuin–Kasteleyn–Ginibre (FKG) inequality is a correlation inequality, a fundamental tool in statistical mechanics and probabilistic combinatorics, due to Cees M. Fortuin, Pieter W. Kasteleyn, and Jean Ginibre (1971). Informally, it says that in many random systems, increasing events are positively correlated, while an increasing and a decreasing event are negatively correlated.

In mathematics, the Pettis integral or Gelfand–Pettis integral, named after Israel M. Gelfand and Billy James Pettis, extends the definition of the Lebesgue integral to vector-valued functions on a measure space, by exploiting duality. The integral was introduced by Gelfand for the case when the measure space is an interval with Lebesgue measure. The integral is also called the weak integral in contrast to the Bochner integral, which is the strong integral.

In mathematics, a distribution function is a real function in measure theory. From every measure on the algebra of Borel sets of real numbers, a distribution function can be constructed, which reflects some of the properties of this measure. Distribution functions are a generalization of distribution functions.

References

  1. ↑ Prékopa, A. (1980). "Logarithmic concave measures and related topics". Stochastic programming (Proc. Internat. Conf., Univ. Oxford, Oxford, 1974). London-New York: Academic Press. pp. 63–82. MR   0592596.
  2. ↑ Borell, C. (1975). "Convex set functions in d-space". Period. Math. Hungar. 6 (2): 111–136. doi:10.1007/BF02018814. MR   0404559.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.