In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.
In geometry, a regular icosahedron is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.
In geometry, an octahedron is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.
In geometry, a tetrahedron, also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra.
The Koch snowflake is a fractal curve and one of the earliest fractals to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled "On a Continuous Curve Without Tangents, Constructible from Elementary Geometry" by the Swedish mathematician Helge von Koch.
In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid with 38 faces: 6 squares and 32 equilateral triangles. It has 60 edges and 24 vertices.
In mathematics, Sperner's lemma is a combinatorial result on colorings of triangulations, analogous to the Brouwer fixed point theorem, which is equivalent to it. It states that every Sperner coloring of a triangulation of an -dimensional simplex contains a cell whose vertices all have different colors.
In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.
In geometry, a disdyakis dodecahedron,, is a Catalan solid with 48 faces and the dual to the Archimedean truncated cuboctahedron. As such it is face-transitive but with irregular face polygons. It resembles an augmented rhombic dodecahedron. Replacing each face of the rhombic dodecahedron with a flat pyramid creates a polyhedron that looks almost like the disdyakis dodecahedron, and is topologically equivalent to it.
Percy Alexander MacMahon was an English mathematician, especially noted in connection with the partitions of numbers and enumerative combinatorics.
The Pyramorphix, also called Pyramorphinx, is a tetrahedral puzzle similar to the Rubik's Cube. It has a total of 8 movable pieces to rearrange, compared to the 20 of the Rubik's Cube. Although it looks like a trivially simple version of the Pyraminx, it is an edge-turning puzzle with the mechanism identical to that of the Pocket Cube.
In combinatorics, the Narayana numbers form a triangular array of natural numbers, called the Narayana triangle, that occur in various counting problems. They are named after Canadian mathematician T. V. Narayana (1930–1987).
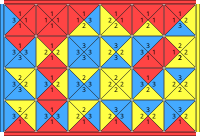
An edge-matching puzzle is a type of tiling puzzle involving tiling an area with polygons whose edges are distinguished with colours or patterns, in such a way that the edges of adjacent tiles match.
The Rubik's Cube is the original and best known of the three-dimensional sequential move puzzles. There have been many virtual implementations of this puzzle in software. It is a natural extension to create sequential move puzzles in more than three dimensions. Although no such puzzle could ever be physically constructed, the rules of how they operate are quite rigorously defined mathematically and are analogous to the rules found in three-dimensional geometry. Hence, they can be simulated by software. As with the mechanical sequential move puzzles, there are records for solvers, although not yet the same degree of competitive organisation.
The V-Cube 6 is a 6×6×6 version of the original Rubik's Cube. The first mass-produced 6×6×6 was invented by Panagiotis Verdes and is produced by the Greek company Verdes Innovations SA. Other such puzzles have since been introduced by a number of Chinese companies, most of which have mechanisms which improve on the original. Unlike the original puzzle, it has no fixed facets: the center facets are free to move to different positions.
The V-Cube 7 is a combination puzzle in the form of a 7×7×7 cube. The first mass-produced 7×7×7 was invented by Panagiotis Verdes and is produced by the Greek company Verdes Innovations SA. Other such puzzles have since been introduced by a number of Chinese companies, some of which have mechanisms which improve on the original. Like the 5×5×5, the V-Cube 7 has both fixed and movable center facets.
The Helicopter Cube is a Rubik's Cube-like puzzle invented by Adam G. Cowan in 2005 and built in 2006. It is also in the shape of a cube. At first glance, the Helicopter Cube may seem like a combination of the 2x2x2 and the Skewb, but it actually cuts differently, and twists around cube edges rather than cube faces. The purpose of the puzzle is to scramble the colors, and then restore them back to their original state of a single color per face.
Serpentiles is the name coined by Kurt N. Van Ness for the hexagonal tiles used in various edge-matching puzzle connection abstract strategy games, such as Psyche-Paths, Kaliko, and Tantrix. For each tile, one to three colors are used to draw paths linking the six sides together in various configurations. Each side is connected to another side by a specific path route and color. Gameplay generally proceeds so that players take turns laying down tiles. During each turn, a tile is laid adjacent to existing tiles so that colored paths are contiguous across tile edges.
Le Trioker is an corner-matching puzzle game played using 25 equilateral triangle-shaped tiles. Each corner is marked with zero, one, two, or three dots and newly placed pieces must match the values on pieces already placed on the game board, similar to the gameplay of the earlier Triominoes.
Triangular Dominoes is a variant of dominoes using equilateral triangle tiles, patented by Franklin H. Richards in 1885. Two versions were made: a starter set of 35 unique tiles, with each side numbered from zero to four pips, and an advanced set of 56 unique tiles, with each side numbered from zero to five pips. In both versions, a wild card "boss" tile was included, making 36 and 57 tiles in each complete set, respectively.
