Related Research Articles

Geodesy is the science of measuring and representing the geometry, gravity, and spatial orientation of the Earth in temporally varying 3D. It is called planetary geodesy when studying other astronomical bodies, such as planets or circumplanetary systems.

In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.
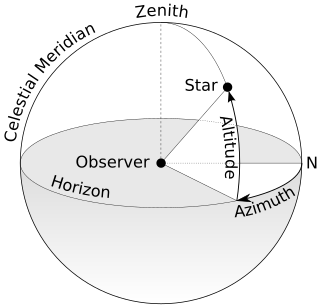
An azimuth is the angular measurement in a spherical coordinate system which represents the horizontal angle from a cardinal direction, most commonly north.

In cartography, a map projection is any of a broad set of transformations employed to represent the curved two-dimensional surface of a globe on a plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography.

In geodesy, the figure of the Earth is the size and shape used to model planet Earth. The kind of figure depends on application, including the precision needed for the model. A spherical Earth is a well-known historical approximation that is satisfactory for geography, astronomy and many other purposes. Several models with greater accuracy have been developed so that coordinate systems can serve the precise needs of navigation, surveying, cadastre, land use, and various other concerns.
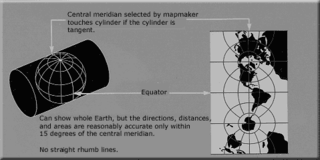
The transverse Mercator map projection is an adaptation of the standard Mercator projection. The transverse version is widely used in national and international mapping systems around the world, including the Universal Transverse Mercator. When paired with a suitable geodetic datum, the transverse Mercator delivers high accuracy in zones less than a few degrees in east-west extent.

The azimuthal equidistant projection is an azimuthal map projection. It has the useful properties that all points on the map are at proportionally correct distances from the center point, and that all points on the map are at the correct azimuth (direction) from the center point. A useful application for this type of projection is a polar projection which shows all meridians as straight, with distances from the pole represented correctly. The flag of the United Nations contains an example of a polar azimuthal equidistant projection.

The equirectangular projection, and which includes the special case of the plate carrée projection, is a simple map projection attributed to Marinus of Tyre, who Ptolemy claims invented the projection about AD 100.

The oblique Mercator map projection is an adaptation of the standard Mercator projection. The oblique version is sometimes used in national mapping systems. When paired with a suitable geodetic datum, the oblique Mercator delivers high accuracy in zones less than a few degrees in arbitrary directional extent.

A Lambert conformal conic projection (LCC) is a conic map projection used for aeronautical charts, portions of the State Plane Coordinate System, and many national and regional mapping systems. It is one of seven projections introduced by Johann Heinrich Lambert in his 1772 publication Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten.

In cartography, the Lambert cylindrical equal-area projection, or Lambert cylindrical projection, is a cylindrical equal-area projection. This projection is undistorted along the equator, which is its standard parallel, but distortion increases rapidly towards the poles. Like any cylindrical projection, it stretches parallels increasingly away from the equator. The poles accrue infinite distortion, becoming lines instead of points.
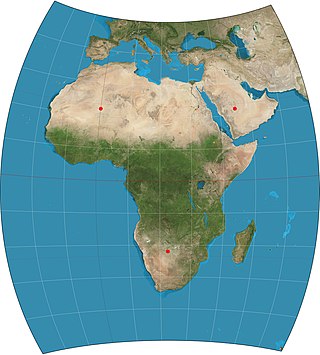
The Chamberlin trimetric projection is a map projection where three points are fixed on the globe and the points on the sphere are mapped onto a plane by triangulation. It was developed in 1946 by Wellman Chamberlin for the National Geographic Society. Chamberlin was chief cartographer for the Society from 1964 to 1971. The projection's principal feature is that it compromises between distortions of area, direction, and distance. A Chamberlin trimetric map therefore gives an excellent overall sense of the region being mapped. Many National Geographic Society maps of single continents use this projection.

The two-point equidistant projection or doubly equidistant projection is a map projection first described by Hans Maurer in 1919 and Charles Close in 1921. It is a generalization of the much simpler azimuthal equidistant projection. In this two-point form, two locus points are chosen by the mapmaker to configure the projection. Distances from the two loci to any other point on the map are correct: that is, they scale to the distances of the same points on the sphere.
In cartography, a conformal map projection is one in which every angle between two curves that cross each other on Earth is preserved in the image of the projection; that is, the projection is a conformal map in the mathematical sense. For example, if two roads cross each other at a 39° angle, their images on a map with a conformal projection cross at a 39° angle.

An Earth ellipsoid or Earth spheroid is a mathematical figure approximating the Earth's form, used as a reference frame for computations in geodesy, astronomy, and the geosciences. Various different ellipsoids have been used as approximations.

The equidistant conic projection is a conic map projection commonly used for maps of small countries as well as for larger regions such as the continental United States that are elongated east-to-west.

The stereographic projection, also known as the planisphere projection or the azimuthal conformal projection, is a conformal map projection whose use dates back to antiquity. Like the orthographic projection and gnomonic projection, the stereographic projection is an azimuthal projection, and when on a sphere, also a perspective projection.

In cartography, an equivalent, authalic, or equal-area projection is a map projection that preserves relative area measure between any and all map regions. Equivalent projections are widely used for thematic maps showing scenario distribution such as population, farmland distribution, forested areas, and so forth, because an equal-area map does not change apparent density of the phenomenon being mapped.
A planetary coordinate system is a generalization of the geographic, geodetic, and the geocentric coordinate systems for planets other than Earth. Similar coordinate systems are defined for other solid celestial bodies, such as in the selenographic coordinates for the Moon. The coordinate systems for almost all of the solid bodies in the Solar System were established by Merton E. Davies of the Rand Corporation, including Mercury, Venus, Mars, the four Galilean moons of Jupiter, and Triton, the largest moon of Neptune.
References
- ↑ Snyder, J. P. (1986). "Conformal Mapping of the Triaxial Ellipsoid". Survey Review. 28 (217): 130–148. doi:10.1179/sre.1985.28.217.130.
- ↑ Pędzich, Paweł (2017). "Equidistant map projections of a triaxial ellipsoid with the use of reduced coordinates". Geodesy and Cartography. 66 (2): 271–290. Bibcode:2017GeCar..66..271P. doi: 10.1515/geocart-2017-0021 .
- ↑ Nyrtsov, Maxim (Winter 2017). "Conic Projections of the Triaxial Ellipsoid: The Projections for Regional Mapping of Celestial Bodies". Cartographica: The International Journal for Geographic Information and Geovisualization. 52 (4): 322–331. doi:10.3138/cart.52.4.2017-0002.
- ↑ Nyrtsov, Maxim V. (2015). "Equal-Area Projections of the Triaxial Ellipsoid: First Time Derivation and Implementation of Cylindrical and Azimuthal Projections for Small Solar System Bodies". The Cartographic Journal. 52 (2): 114–124. doi:10.1080/00087041.2015.1119471. S2CID 124797916 . Retrieved 9 February 2019.
- ↑ Nyrtsov, Maxim V. (2014). "Jacobi Conformal Projection of the Triaxial Ellipsoid: New Projection for Mapping of Small Celestial Bodies". Cartography from Pole to Pole. Springer, Berlin, Heidelberg. pp. 235–246. ISBN 978-3-642-32617-2.