In economics, specifically general equilibrium theory, a perfect market, also known as an atomistic market, is defined by several idealizing conditions, collectively called perfect competition, or atomistic competition. In theoretical models where conditions of perfect competition hold, it has been demonstrated that a market will reach an equilibrium in which the quantity supplied for every product or service, including labor, equals the quantity demanded at the current price. This equilibrium would be a Pareto optimum.

In economics, profit maximization is the short run or long run process by which a firm may determine the price, input and output levels that will lead to the highest possible total profit. In neoclassical economics, which is currently the mainstream approach to microeconomics, the firm is assumed to be a "rational agent" which wants to maximize its total profit, which is the difference between its total revenue and its total cost.

The break-even point (BEP) in economics, business—and specifically cost accounting—is the point at which total cost and total revenue are equal, i.e. "even". In layman's terms, after all costs are paid for there is neither profit nor loss. In economics specifically, the term has a broader definition; even if there is no net loss or gain, and one has "broken even", opportunity costs have been covered and capital has received the risk-adjusted, expected return. The break-even analysis was developed by Karl Bücher and Johann Friedrich Schär.
In economics, the marginal cost is the change in the total cost that arises when the quantity produced is increased, i.e. the cost of producing additional quantity. In some contexts, it refers to an increment of one unit of output, and in others it refers to the rate of change of total cost as output is increased by an infinitesimal amount. As Figure 1 shows, the marginal cost is measured in dollars per unit, whereas total cost is in dollars, and the marginal cost is the slope of the total cost, the rate at which it increases with output. Marginal cost is different from average cost, which is the total cost divided by the number of units produced.

In economics, a production function gives the technological relation between quantities of physical inputs and quantities of output of goods. The production function is one of the key concepts of mainstream neoclassical theories, used to define marginal product and to distinguish allocative efficiency, a key focus of economics. One important purpose of the production function is to address allocative efficiency in the use of factor inputs in production and the resulting distribution of income to those factors, while abstracting away from the technological problems of achieving technical efficiency, as an engineer or professional manager might understand it.
The classical general equilibrium model aims to describe the economy by aggregating the behavior of individuals and firms. Note that the classical general equilibrium model is unrelated to classical economics, and was instead developed within neoclassical economics beginning in the late 19th century.

In economics and in particular neoclassical economics, the marginal product or marginal physical productivity of an input is the change in output resulting from employing one more unit of a particular input, assuming that the quantities of other inputs are kept constant.
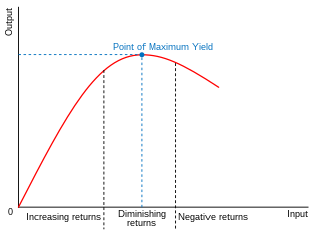
In economics, diminishing returns are the decrease in marginal (incremental) output of a production process as the amount of a single factor of production is incrementally increased, holding all other factors of production equal. The law of diminishing returns states that in productive processes, increasing a factor of production by one unit, while holding all other production factors constant, will at some point return a lower unit of output per incremental unit of input. The law of diminishing returns does not cause a decrease in overall production capabilities, rather it defines a point on a production curve whereby producing an additional unit of output will result in a loss and is known as negative returns. Under diminishing returns, output remains positive, but productivity and efficiency decrease.

Marginal revenue is a central concept in microeconomics that describes the additional total revenue generated by increasing product sales by 1 unit. Marginal revenue is the increase in revenue from the sale of one additional unit of product, i.e., the revenue from the sale of the last unit of product. It can be positive or negative. Marginal revenue is an important concept in vendor analysis. To derive the value of marginal revenue, it is required to examine the difference between the aggregate benefits a firm received from the quantity of a good and service produced last period and the current period with one extra unit increase in the rate of production. Marginal revenue is a fundamental tool for economic decision making within a firm's setting, together with marginal cost to be considered.
Cournot competition is an economic model used to describe an industry structure in which companies compete on the amount of output they will produce, which they decide on independently of each other and at the same time. It is named after Antoine Augustin Cournot (1801–1877) who was inspired by observing competition in a spring water duopoly. It has the following features:
The Ramsey problem, or Ramsey pricing, or Ramsey–Boiteux pricing, is a second-best policy problem concerning what prices a public monopoly should charge for the various products it sells in order to maximize social welfare while earning enough revenue to cover its fixed costs.
In economics, a cost curve is a graph of the costs of production as a function of total quantity produced. In a free market economy, productively efficient firms optimize their production process by minimizing cost consistent with each possible level of production, and the result is a cost curve. Profit-maximizing firms use cost curves to decide output quantities. There are various types of cost curves, all related to each other, including total and average cost curves; marginal cost curves, which are equal to the differential of the total cost curves; and variable cost curves. Some are applicable to the short run, others to the long run.
The Solow–Swan model or exogenous growth model is an economic model of long-run economic growth. It attempts to explain long-run economic growth by looking at capital accumulation, labor or population growth, and increases in productivity largely driven by technological progress. At its core, it is an aggregate production function, often specified to be of Cobb–Douglas type, which enables the model "to make contact with microeconomics". The model was developed independently by Robert Solow and Trevor Swan in 1956, and superseded the Keynesian Harrod–Domar model.
The Harrod–Domar model is a Keynesian model of economic growth. It is used in development economics to explain an economy's growth rate in terms of the level of saving and of capital. It suggests that there is no natural reason for an economy to have balanced growth. The model was developed independently by Roy F. Harrod in 1939, and Evsey Domar in 1946, although a similar model had been proposed by Gustav Cassel in 1924. The Harrod–Domar model was the precursor to the exogenous growth model.
The Dual Sector model, or the Lewis model, is a model in developmental economics that explains the growth of a developing economy in terms of a labour transition between two sectors, the subsistence or traditional agricultural sector and the capitalist or modern industrial sector.
In economics, the marginal product of capital (MPK) is the additional production that a firm experiences when it adds an extra unit of input. It is a feature of the production function, alongside the labour input.
In economics, a monopsony is a market structure in which a single buyer substantially controls the market as the major purchaser of goods and services offered by many would-be sellers. The microeconomic theory of monopsony assumes a single entity to have market power over all sellers as the only purchaser of a good or service. This is a similar power to that of a monopolist, which can influence the price for its buyers in a monopoly, where multiple buyers have only one seller of a good or service available to purchase from.

In economics, a factor market is a market where factors of production are bought and sold. Factor markets allocate factors of production, including land, labour and capital, and distribute income to the owners of productive resources, such as wages, rents, etc.
In economics, the marginal product of labor (MPL) is the change in output that results from employing an added unit of labor. It is a feature of the production function and depends on the amounts of physical capital and labor already in use.

In microeconomics, a monopoly price is set by a monopoly. A monopoly occurs when a firm lacks any viable competition and is the sole producer of the industry's product. Because a monopoly faces no competition, it has absolute market power and can set a price above the firm's marginal cost.





















