Growth accounting is a procedure used in economics to measure the contribution of different factors to economic growth and to indirectly compute the rate of technological progress, measured as a residual, in an economy. Growth accounting decomposes the growth rate of an economy's total output into that which is due to increases in the contributing amount of the factors used—usually the increase in the amount of capital and labor—and that which cannot be accounted for by observable changes in factor utilization. The unexplained part of growth in GDP is then taken to represent increases in productivity or a measure of broadly defined technological progress.

In economics, profit maximization is the short run or long run process by which a firm may determine the price, input and output levels that will lead to the highest possible total profit. In neoclassical economics, which is currently the mainstream approach to microeconomics, the firm is assumed to be a "rational agent" which wants to maximize its total profit, which is the difference between its total revenue and its total cost.
In economics, the marginal cost is the change in the total cost that arises when the quantity produced is increased, i.e. the cost of producing additional quantity. In some contexts, it refers to an increment of one unit of output, and in others it refers to the rate of change of total cost as output is increased by an infinitesimal amount. As Figure 1 shows, the marginal cost is measured in dollars per unit, whereas total cost is in dollars, and the marginal cost is the slope of the total cost, the rate at which it increases with output. Marginal cost is different from average cost, which is the total cost divided by the number of units produced.

In economics and econometrics, the Cobb–Douglas production function is a particular functional form of the production function, widely used to represent the technological relationship between the amounts of two or more inputs and the amount of output that can be produced by those inputs. The Cobb–Douglas form was developed and tested against statistical evidence by Charles Cobb and Paul Douglas between 1927 and 1947; according to Douglas, the functional form itself was developed earlier by Philip Wicksteed.

In economics, a production function gives the technological relation between quantities of physical inputs and quantities of output of goods. The production function is one of the key concepts of mainstream neoclassical theories, used to define marginal product and to distinguish allocative efficiency, a key focus of economics. One important purpose of the production function is to address allocative efficiency in the use of factor inputs in production and the resulting distribution of income to those factors, while abstracting away from the technological problems of achieving technical efficiency, as an engineer or professional manager might understand it.
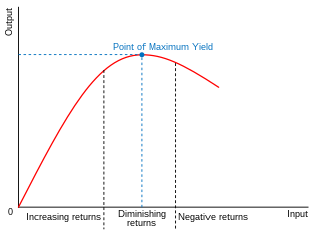
In economics, diminishing returns are the decrease in marginal (incremental) output of a production process as the amount of a single factor of production is incrementally increased, holding all other factors of production equal. The law of diminishing returns states that in productive processes, increasing a factor of production by one unit, while holding all other production factors constant, will at some point return a lower unit of output per incremental unit of input. The law of diminishing returns does not cause a decrease in overall production capabilities, rather it defines a point on a production curve whereby producing an additional unit of output will result in a loss and is known as negative returns. Under diminishing returns, output remains positive, but productivity and efficiency decrease.
In machine learning, backpropagation is a gradient estimation method commonly used for training neural networks to compute the network parameter updates.
The marginal revenue productivity theory of wages is a model of wage levels in which they set to match to the marginal revenue product of labor, , which is the increment to revenues caused by the increment to output produced by the last laborer employed. In a model, this is justified by an assumption that the firm is profit-maximizing and thus would employ labor only up to the point that marginal labor costs equal the marginal revenue generated for the firm. This is a model of the neoclassical economics type.
In economics, a cost curve is a graph of the costs of production as a function of total quantity produced. In a free market economy, productively efficient firms optimize their production process by minimizing cost consistent with each possible level of production, and the result is a cost curve. Profit-maximizing firms use cost curves to decide output quantities. There are various types of cost curves, all related to each other, including total and average cost curves; marginal cost curves, which are equal to the differential of the total cost curves; and variable cost curves. Some are applicable to the short run, others to the long run.
The Solow residual is a number describing empirical productivity growth in an economy from year to year and decade to decade. Robert Solow, the Nobel Memorial Prize in Economic Sciences-winning economist, defined rising productivity as rising output with constant capital and labor input. It is a "residual" because it is the part of growth that is not accounted for by measures of capital accumulation or increased labor input. Increased physical throughput – i.e. environmental resources – is specifically excluded from the calculation; thus some portion of the residual can be ascribed to increased physical throughput. The example used is for the intracapital substitution of aluminium fixtures for steel during which the inputs do not alter. This differs in almost every other economic circumstance in which there are many other variables. The Solow residual is procyclical and measures of it are now called the rate of growth of multifactor productivity or total factor productivity, though Solow (1957) did not use these terms.
The Solow–Swan model or exogenous growth model is an economic model of long-run economic growth. It attempts to explain long-run economic growth by looking at capital accumulation, labor or population growth, and increases in productivity largely driven by technological progress. At its core, it is an aggregate production function, often specified to be of Cobb–Douglas type, which enables the model "to make contact with microeconomics". The model was developed independently by Robert Solow and Trevor Swan in 1956, and superseded the Keynesian Harrod–Domar model.
The Harrod–Domar model is a Keynesian model of economic growth. It is used in development economics to explain an economy's growth rate in terms of the level of saving and of capital. It suggests that there is no natural reason for an economy to have balanced growth. The model was developed independently by Roy F. Harrod in 1939, and Evsey Domar in 1946, although a similar model had been proposed by Gustav Cassel in 1924. The Harrod–Domar model was the precursor to the exogenous growth model.
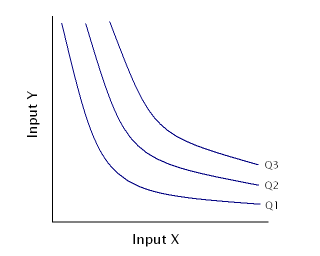
In microeconomic theory, the marginal rate of technical substitution (MRTS)—or technical rate of substitution (TRS)—is the amount by which the quantity of one input has to be reduced when one extra unit of another input is used, so that output remains constant.
The Ramsey–Cass–Koopmans model, or Ramsey growth model, is a neoclassical model of economic growth based primarily on the work of Frank P. Ramsey, with significant extensions by David Cass and Tjalling Koopmans. The Ramsey–Cass–Koopmans model differs from the Solow–Swan model in that the choice of consumption is explicitly microfounded at a point in time and so endogenizes the savings rate. As a result, unlike in the Solow–Swan model, the saving rate may not be constant along the transition to the long run steady state. Another implication of the model is that the outcome is Pareto optimal or Pareto efficient.

In economics, supply is the amount of a resource that firms, producers, labourers, providers of financial assets, or other economic agents are willing and able to provide to the marketplace or to an individual. Supply can be in produced goods, labour time, raw materials, or any other scarce or valuable object. Supply is often plotted graphically as a supply curve, with the price per unit on the vertical axis and quantity supplied as a function of price on the horizontal axis. This reversal of the usual position of the dependent variable and the independent variable is an unfortunate but standard convention.
In economics, the marginal product of capital (MPK) is the additional production that a firm experiences when it adds an extra unit of input. It is a feature of the production function, alongside the labour input.
In economics, the marginal product of labor (MPL) is the change in output that results from employing an added unit of labor. It is a feature of the production function and depends on the amounts of physical capital and labor already in use.
The AK model of economic growth is an endogenous growth model used in the theory of economic growth, a subfield of modern macroeconomics. In the 1980s it became progressively clearer that the standard neoclassical exogenous growth models were theoretically unsatisfactory as tools to explore long run growth, as these models predicted economies without technological change and thus they would eventually converge to a steady state, with zero per capita growth. A fundamental reason for this is the diminishing return of capital; the key property of AK endogenous-growth model is the absence of diminishing returns to capital. In lieu of the diminishing returns of capital implied by the usual parameterizations of a Cobb–Douglas production function, the AK model uses a linear model where output is a linear function of capital. Its appearance in most textbooks is to introduce endogenous growth theory.
In the technological theory of social production, the growth of output, measured in money units, is related to achievements in technological consumption of labour and energy. This theory is based on concepts of classical political economy and neo-classical economics and appears to be a generalisation of the known economic models, such as the neo-classical model of economic growth and input-output model.













