Related Research Articles

In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary of non-zero length. It was the first major theorem to be proved using a computer. Initially, this proof was not accepted by all mathematicians because the computer-assisted proof was infeasible for a human to check by hand. The proof has gained wide acceptance since then, although some doubts remain.
In graph theory, the girth of an undirected graph is the length of a shortest cycle contained in the graph. If the graph does not contain any cycles, its girth is defined to be infinity. For example, a 4-cycle (square) has girth 4. A grid has girth 4 as well, and a triangular mesh has girth 3. A graph with girth four or more is triangle-free.
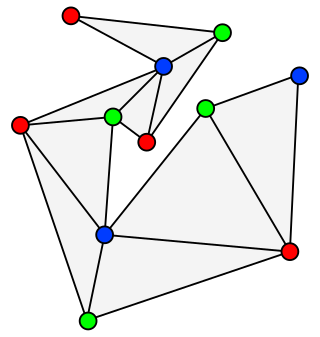
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.
In graph theory, a branch of mathematics, list coloring is a type of graph coloring where each vertex can be restricted to a list of allowed colors. It was first studied in the 1970s in independent papers by Vizing and by Erdős, Rubin, and Taylor.

In the mathematical field of graph theory, a snark is an undirected graph with exactly three edges per vertex whose edges cannot be colored with only three colors. In order to avoid trivial cases, snarks are often restricted to have additional requirements on their connectivity and on the length of their cycles. Infinitely many snarks exist.

In graph theory, the Hadwiger conjecture states that if is loopless and has no minor then its chromatic number satisfies . It is known to be true for . The conjecture is a generalization of the four-color theorem and is considered to be one of the most important and challenging open problems in the field.

The five color theorem is a result from graph theory that given a plane separated into regions, such as a political map of the countries of the world, the regions may be colored using no more than five colors in such a way that no two adjacent regions receive the same color.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings in a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.
In graph theory, Vizing's theorem states that every simple undirected graph may be edge colored using a number of colors that is at most one larger than the maximum degree Δ of the graph. At least Δ colors are always necessary, so the undirected graphs may be partitioned into two classes: "class one" graphs for which Δ colors suffice, and "class two" graphs for which Δ + 1 colors are necessary. A more general version of Vizing's theorem states that every undirected multigraph without loops can be colored with at most Δ+µ colors, where µ is the multiplicity of the multigraph. The theorem is named for Vadim G. Vizing who published it in 1964.
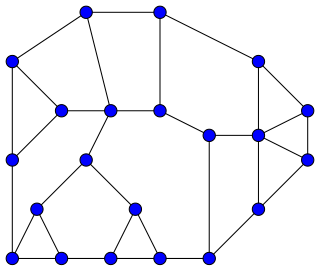
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle. The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross, and the cycle connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.
In graph theory, the De Bruijn–Erdős theorem relates graph coloring of an infinite graph to the same problem on its finite subgraphs. It states that, when all finite subgraphs can be colored with colors, the same is true for the whole graph. The theorem was proved by Nicolaas Govert de Bruijn and Paul Erdős, after whom it is named.

In the mathematical field of graph theory, Grötzsch's theorem is the statement that every triangle-free planar graph can be colored with only three colors. According to the four-color theorem, every graph that can be drawn in the plane without edge crossings can have its vertices colored using at most four different colors, so that the two endpoints of every edge have different colors, but according to Grötzsch's theorem only three colors are needed for planar graphs that do not contain three mutually adjacent vertices.

In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate. The degeneracy of a graph is a measure of how sparse it is, and is within a constant factor of other sparsity measures such as the arboricity of a graph.

In topological graph theory, a 1-planar graph is a graph that can be drawn in the Euclidean plane in such a way that each edge has at most one crossing point, where it crosses a single additional edge. If a 1-planar graph, one of the most natural generalizations of planar graphs, is drawn that way, the drawing is called a 1-plane graph or 1-planar embedding of the graph.
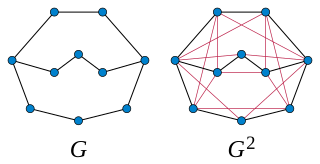
In graph theory, a branch of mathematics, the kth powerGk of an undirected graph G is another graph that has the same set of vertices, but in which two vertices are adjacent when their distance in G is at most k. Powers of graphs are referred to using terminology similar to that of exponentiation of numbers: G2 is called the square of G, G3 is called the cube of G, etc.
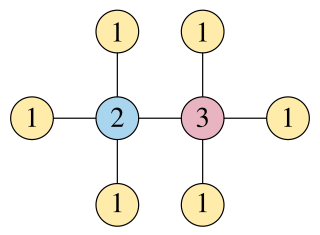
In graph theory, a sum coloring of a graph is a labeling of its vertices by positive integers, with no two adjacent vertices having equal labels, that minimizes the sum of the labels. The minimum sum that can be achieved is called the chromatic sum of the graph. Chromatic sums and sum coloring were introduced by Supowit in 1987 using non-graph-theoretic terminology, and first studied in graph theoretic terms by Ewa Kubicka in her 1989 doctoral thesis.
Maria-Viktoria Hasse was a German mathematician who became the first female professor in the faculty of mathematics and science at TU Dresden. She wrote books on set theory and category theory, and is known as one of the namesakes of the Gallai–Hasse–Roy–Vitaver theorem in graph coloring.
References
- ↑ Prof. Dr. rer. nat. habil. Margit Voigt, University of Applied Sciences Dresden, retrieved 2019-10-01
- ↑ Margit Voigt at the Mathematics Genealogy Project
- 1 2 Aigner, Martin; Ziegler, Günter M. (1999), "Chapter 25: Five-coloring plane graphs", Proofs from The Book, Berlin: Springer-Verlag, pp. 161–164, ISBN 3-540-63698-6, MR 1723092
- ↑ Chartrand, Gary; Lesniak, Linda; Zhang, Ping (2011), Graphs & Digraphs (5th ed.), Boca Raton, FL: CRC Press, p. 378, ISBN 978-1-4398-2627-0, MR 2766107
- ↑ Chen, Louis Hsiao Yun (2001), Challenges for the Twenty-first Century, World Scientific, p. 191, ISBN 9789810246464