In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces. They are sometimes called Lebesgue spaces, named after Henri Lebesgue, although according to the Bourbaki group they were first introduced by Frigyes Riesz.
In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces.
In probability theory, the conditional expectation, conditional expected value, or conditional mean of a random variable is its expected value evaluated with respect to the conditional probability distribution. If the random variable can take on only a finite number of values, the "conditions" are that the variable can only take on a subset of those values. More formally, in the case when the random variable is defined over a discrete probability space, the "conditions" are a partition of this probability space.
The spectrum of a linear operator that operates on a Banach space is a fundamental concept of functional analysis. The spectrum consists of all scalars such that the operator does not have a bounded inverse on . The spectrum has a standard decomposition into three parts:

In mathematics, mixing is an abstract concept originating from physics: the attempt to describe the irreversible thermodynamic process of mixing in the everyday world: e.g. mixing paint, mixing drinks, industrial mixing.
In mathematics, ergodicity expresses the idea that a point of a moving system, either a dynamical system or a stochastic process, will eventually visit all parts of the space that the system moves in, in a uniform and random sense. This implies that the average behavior of the system can be deduced from the trajectory of a "typical" point. Equivalently, a sufficiently large collection of random samples from a process can represent the average statistical properties of the entire process. Ergodicity is a property of the system; it is a statement that the system cannot be reduced or factored into smaller components. Ergodic theory is the study of systems possessing ergodicity.
In mathematics, the disintegration theorem is a result in measure theory and probability theory. It rigorously defines the idea of a non-trivial "restriction" of a measure to a measure zero subset of the measure space in question. It is related to the existence of conditional probability measures. In a sense, "disintegration" is the opposite process to the construction of a product measure.
In probability theory relating to stochastic processes, a Feller process is a particular kind of Markov process.
In mathematics, uniform integrability is an important concept in real analysis, functional analysis and measure theory, and plays a vital role in the theory of martingales.
In probability theory, a random measure is a measure-valued random element. Random measures are for example used in the theory of random processes, where they form many important point processes such as Poisson point processes and Cox processes.
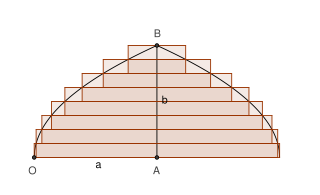
In mathematics, the layer cake representation of a non-negative, real-valued measurable function defined on a measure space is the formula
In the mathematical theory of probability, a Borel right process, named after Émile Borel, is a particular kind of continuous-time random process.
In mathematics – specifically, in stochastic analysis – an Itô diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation used in physics to describe the Brownian motion of a particle subjected to a potential in a viscous fluid. Itô diffusions are named after the Japanese mathematician Kiyosi Itô.
In mathematics — specifically, in stochastic analysis — the infinitesimal generator of a Feller process is a Fourier multiplier operator that encodes a great deal of information about the process.
In real analysis and measure theory, the Vitali convergence theorem, named after the Italian mathematician Giuseppe Vitali, is a generalization of the better-known dominated convergence theorem of Henri Lebesgue. It is a characterization of the convergence in Lp in terms of convergence in measure and a condition related to uniform integrability.
In probability theory, a Markov kernel is a map that in the general theory of Markov processes plays the role that the transition matrix does in the theory of Markov processes with a finite state space.
In potential theory and functional analysis, Dirichlet forms generalize the Laplacian. Dirichlet forms can be defined on any measure space, without the need for mentioning partial derivatives. This allows mathematicians to study the Laplace equation and heat equation on spaces that are not manifolds, for example, fractals. The benefit on these spaces is that one can do this without needing a gradient operator, and in particular, one can even weakly define a "Laplacian" in this manner if starting with the Dirichlet form.
A Markov chain on a measurable state space is a discrete-time-homogeneous Markov chain with a measurable space as state space.
In mathematics, the Poisson boundary is a measure space associated to a random walk. It is an object designed to encode the asymptotic behaviour of the random walk, i.e. how trajectories diverge when the number of steps goes to infinity. Despite being called a boundary it is in general a purely measure-theoretical object and not a boundary in the topological sense. However, in the case where the random walk is on a topological space the Poisson boundary can be related to the Martin boundary, which is an analytic construction yielding a genuine topological boundary. Both boundaries are related to harmonic functions on the space via generalisations of the Poisson formula.
In functional analysis, double operator integrals (DOI) are integrals of the form







































