Related Research Articles
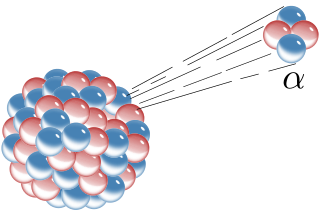
Alpha decay or α-decay is a type of radioactive decay in which an atomic nucleus emits an alpha particle and thereby transforms or 'decays' into a different atomic nucleus, with a mass number that is reduced by four and an atomic number that is reduced by two. An alpha particle is identical to the nucleus of a helium-4 atom, which consists of two protons and two neutrons. It has a charge of +2 e and a mass of 4 Da. For example, uranium-238 decays to form thorium-234.

The neutron is a subatomic particle, symbol
n
or
n0
, which has a neutral charge, and a mass slightly greater than that of a proton. Protons and neutrons constitute the nuclei of atoms. Since protons and neutrons behave similarly within the nucleus, and each has a mass of approximately one dalton, they are both referred to as nucleons. Their properties and interactions are described by nuclear physics. Protons and neutrons are not elementary particles; each is composed of three quarks.

Nuclear physics is the field of physics that studies atomic nuclei and their constituents and interactions, in addition to the study of other forms of nuclear matter.

Nuclear fusion is a reaction in which two or more atomic nuclei, usually deuterium and tritium, combine to form one or more different atomic nuclei and subatomic particles. The difference in mass between the reactants and products is manifested as either the release or absorption of energy. This difference in mass arises due to the difference in nuclear binding energy between the atomic nuclei before and after the reaction. Nuclear fusion is the process that powers active or main-sequence stars and other high-magnitude stars, where large amounts of energy are released.

In physics and chemistry, a nucleon is either a proton or a neutron, considered in its role as a component of an atomic nucleus. The number of nucleons in a nucleus defines the atom's mass number.
In physics and chemistry, binding energy is the smallest amount of energy required to remove a particle from a system of particles or to disassemble a system of particles into individual parts. In the former meaning the term is predominantly used in condensed matter physics, atomic physics, and chemistry, whereas in nuclear physics the term separation energy is used.
In nuclear engineering, fissile material is material that can undergo nuclear fission when struck by a neutron of low energy. A self-sustaining thermal chain reaction can only be achieved with fissile material. The predominant neutron energy in a system may be typified by either slow neutrons or fast neutrons. Fissile material can be used to fuel thermal-neutron reactors, fast-neutron reactors and nuclear explosives.
In astrophysics, silicon burning is a very brief sequence of nuclear fusion reactions that occur in massive stars with a minimum of about 8–11 solar masses. Silicon burning is the final stage of fusion for massive stars that have run out of the fuels that power them for their long lives in the main sequence on the Hertzsprung–Russell diagram. It follows the previous stages of hydrogen, helium, carbon, neon and oxygen burning processes.

In nuclear physics and nuclear chemistry, a nuclear reaction is a process in which two nuclei, or a nucleus and an external subatomic particle, collide to produce one or more new nuclides. Thus, a nuclear reaction must cause a transformation of at least one nuclide to another. If a nucleus interacts with another nucleus or particle and they then separate without changing the nature of any nuclide, the process is simply referred to as a type of nuclear scattering, rather than a nuclear reaction.

In nuclear physics, a magic number is a number of nucleons such that they are arranged into complete shells within the atomic nucleus. As a result, atomic nuclei with a 'magic' number of protons or neutrons are much more stable than other nuclei. The seven most widely recognized magic numbers as of 2019 are 2, 8, 20, 28, 50, 82, and 126.

The mass number (symbol A, from the German word: Atomgewicht, "atomic weight"), also called atomic mass number or nucleon number, is the total number of protons and neutrons (together known as nucleons) in an atomic nucleus. It is approximately equal to the atomic (also known as isotopic) mass of the atom expressed in atomic mass units. Since protons and neutrons are both baryons, the mass number A is identical with the baryon number B of the nucleus (and also of the whole atom or ion). The mass number is different for each isotope of a given chemical element, and the difference between the mass number and the atomic number Z gives the number of neutrons (N) in the nucleus: N = A − Z.

In nuclear physics, the semi-empirical mass formula (SEMF) is used to approximate the mass of an atomic nucleus from its number of protons and neutrons. As the name suggests, it is based partly on theory and partly on empirical measurements. The formula represents the liquid-drop model proposed by George Gamow, which can account for most of the terms in the formula and gives rough estimates for the values of the coefficients. It was first formulated in 1935 by German physicist Carl Friedrich von Weizsäcker, and although refinements have been made to the coefficients over the years, the structure of the formula remains the same today.

The nuclear force is a force that acts between the protons and neutrons of atoms. Neutrons and protons, both nucleons, are affected by the nuclear force almost identically. Since protons have charge +1 e, they experience an electric force that tends to push them apart, but at short range the attractive nuclear force is strong enough to overcome the electromagnetic force. The nuclear force binds nucleons into atomic nuclei.

Cluster decay, also named heavy particle radioactivity, heavy ion radioactivity or heavy cluster decay, is a rare type of nuclear decay in which an atomic nucleus emits a small "cluster" of neutrons and protons, more than in an alpha particle, but less than a typical binary fission fragment. Ternary fission into three fragments also produces products in the cluster size. The loss of protons from the parent nucleus changes it to the nucleus of a different element, the daughter, with a mass number Ad = A − Ae and atomic number Zd = Z − Ze, where Ae = Ne + Ze. For example:
Technetium (43Tc) is one of the two elements with Z < 83 that have no stable isotopes; the other such element is promethium. It is primarily artificial, with only trace quantities existing in nature produced by spontaneous fission or neutron capture by molybdenum. The first isotopes to be synthesized were 97Tc and 99Tc in 1936, the first artificial element to be produced. The most stable radioisotopes are 97Tc, 98Tc, and 99Tc.

Nuclear binding energy in experimental physics is the minimum energy that is required to disassemble the nucleus of an atom into its constituent protons and neutrons, known collectively as nucleons. The binding energy for stable nuclei is always a positive number, as the nucleus must gain energy for the nucleons to move apart from each other. Nucleons are attracted to each other by the strong nuclear force. In theoretical nuclear physics, the nuclear binding energy is considered a negative number. In this context it represents the energy of the nucleus relative to the energy of the constituent nucleons when they are infinitely far apart. Both the experimental and theoretical views are equivalent, with slightly different emphasis on what the binding energy means.

In nuclear physics, the valley of stability is a characterization of the stability of nuclides to radioactivity based on their binding energy. Nuclides are composed of protons and neutrons. The shape of the valley refers to the profile of binding energy as a function of the numbers of neutrons and protons, with the lowest part of the valley corresponding to the region of most stable nuclei. The line of stable nuclides down the center of the valley of stability is known as the line of beta stability. The sides of the valley correspond to increasing instability to beta decay. The decay of a nuclide becomes more energetically favorable the further it is from the line of beta stability. The boundaries of the valley correspond to the nuclear drip lines, where nuclides become so unstable they emit single protons or single neutrons. Regions of instability within the valley at high atomic number also include radioactive decay by alpha radiation or spontaneous fission. The shape of the valley is roughly an elongated paraboloid corresponding to the nuclide binding energies as a function of neutron and atomic numbers.
Nickel-62 is an isotope of nickel having 28 protons and 34 neutrons.
The atomic mass (ma or m) is the mass of an atom. Although the SI unit of mass is the kilogram (symbol: kg), atomic mass is often expressed in the non-SI unit dalton (symbol: Da) – equivalently, unified atomic mass unit (u). 1 Da is defined as 1⁄12 of the mass of a free carbon-12 atom at rest in its ground state. The protons and neutrons of the nucleus account for nearly all of the total mass of atoms, with the electrons and nuclear binding energy making minor contributions. Thus, the numeric value of the atomic mass when expressed in daltons has nearly the same value as the mass number. Conversion between mass in kilograms and mass in daltons can be done using the atomic mass constant .

The nuclear drip line is the boundary beyond which atomic nuclei are unbound with respect to the emission of a proton or neutron.
References
- Krane, K. S (1987). Introductory Nuclear Physics. John Wiley & Sons. ISBN 0-471-80553-X.
- Tipler, P. A; Llewellyn, R. A. (2004). Modern Physics. W. H. Freeman and Company. ISBN 0-7167-4345-0.