 | This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations .(June 2024) |
Meridian altitude is a method of celestial navigation to calculate an observer's latitude. It notes the altitude angle of an astronomical object above the horizon at culmination.
Meridian altitude is the simplest calculation of celestial navigation, in which an observer determines his latitude by measuring the altitude of an astronomical object at the time of its meridian contact. A meridian contact is the moment when the object contacts the observer's meridian, i.e. the imaginary line running north–south and through the zenith, nadir, and celestial poles. This is usually done with the equinox Sun at solar noon to determine the observer's latitude, but can be done with any celestial object. Solar noon is the time when the Sun contacts the meridian.
Imagine that the equinox Sun is overhead (at the zenith) at a point on the Equator (latitude 0°), and Observer A is standing at this point – the subsolar point. If he were to measure the height of the Sun above the horizon with a sextant, he would find that the altitude of the Sun was 90°. By subtracting this figure from 90°, he would find that the zenith distance of the Sun is 0°, which is the same as his latitude. If Observer B is standing at one of the geographical poles (latitude 90°N or 90°S), he would see the Sun on the horizon at an altitude of 0°. By subtracting this from 90°, he would find that the zenith distance is 90°, which is his latitude. Observer C at the same time is at latitude 20°N on the same meridian, i.e. on the same longitude as Observer A. His measured altitude would be 70°, and subtracting this from 90° gives a 20° zenith distance, which in turn is his latitude. In short, the zenith distance of a celestial object at meridian altitude is the difference in latitude between it and the observer.
The estimated time of meridian altitude of the heavenly object is extracted from the nautical almanac. A few minutes before this time the observer starts observing the altitude of the object with a sextant. The altitude of the object will be increasing and the observer will continually adjust the sextant to keep the reflected image of the object on the horizon. As the object passes the meridian a maximum altitude will be observed. The time in UTC of this is observed.
The altitude obtained is corrected for dip (the error caused by the observers height above the sea) and refraction to obtain the true altitude of the object above the horizon. This is then subtracted from 90° to obtain the angular distance from the position directly above to obtain the zenith distance.
A further correction must then be taken into account to counter the "wobble" of the earth's spin and rotation relative to the sun and planets. This is given in the declination for the body on a particular day in the year (also taken from the nautical almanac). If the declination of the body is in the opposite hemisphere (ie if you are in the northern hemisphere and the declination is in the southern hemisphere) then the declination must be subtracted from your true zenith distance, otherwise the declination is added.
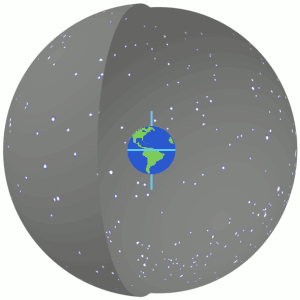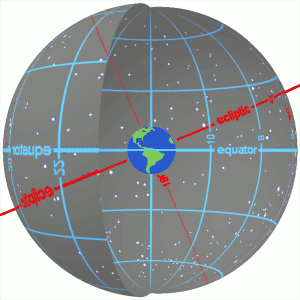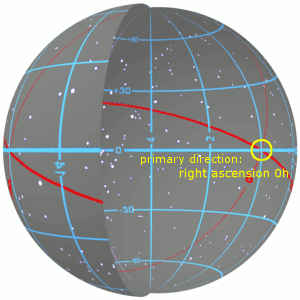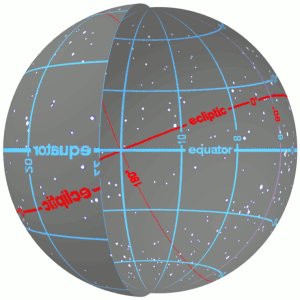
In astronomy, declination is one of the two angles that locate a point on the celestial sphere in the equatorial coordinate system, the other being hour angle. The declination angle is measured north (positive) or south (negative) of the celestial equator, along the hour circle passing through the point in question.
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another. The field of navigation includes four general categories: land navigation, marine navigation, aeronautic navigation, and space navigation.
Right ascension is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the March equinox to the point in question above the Earth. When paired with declination, these astronomical coordinates specify the location of a point on the celestial sphere in the equatorial coordinate system.
A sextant is a doubly reflecting navigation instrument that measures the angular distance between two visible objects. The primary use of a sextant is to measure the angle between an astronomical object and the horizon for the purposes of celestial navigation.
In astronomy, coordinate systems are used for specifying positions of celestial objects relative to a given reference frame, based on physical reference points available to a situated observer. Coordinate systems in astronomy can specify an object's relative position in three-dimensional space or plot merely by its direction on a celestial sphere, if the object's distance is unknown or trivial.
The equatorial coordinate system is a celestial coordinate system widely used to specify the positions of celestial objects. It may be implemented in spherical or rectangular coordinates, both defined by an origin at the centre of Earth, a fundamental plane consisting of the projection of Earth's equator onto the celestial sphere, a primary direction towards the March equinox, and a right-handed convention.
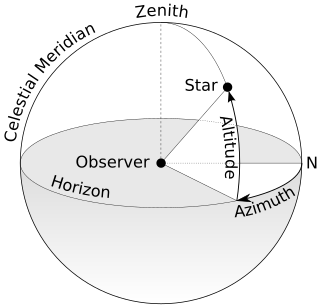
The horizontal coordinate system is a celestial coordinate system that uses the observer's local horizon as the fundamental plane to define two angles of a spherical coordinate system: altitude and azimuth. Therefore, the horizontal coordinate system is sometimes called the az/el system, the alt/az system, or the alt-azimuth system, among others. In an altazimuth mount of a telescope, the instrument's two axes follow altitude and azimuth.
In astronomy and celestial navigation, the hour angle is the dihedral angle between the meridian plane and the hour circle.
An astrolabe is an astronomical instrument dating to ancient times. It serves as a star chart and physical model of visible heavenly bodies. Its various functions also make it an elaborate inclinometer and an analog calculation device capable of working out several kinds of problems in astronomy. In its simplest form it is a metal disc with a pattern of wires, cutouts, and perforations that allows a user to calculate astronomical positions precisely. It is able to measure the altitude above the horizon of a celestial body, day or night; it can be used to identify stars or planets, to determine local latitude given local time, to survey, or to triangulate. It was used in classical antiquity, the Islamic Golden Age, the European Middle Ages and the Age of Discovery for all these purposes.
Celestial navigation, also known as astronavigation, is the practice of position fixing using stars and other celestial bodies that enables a navigator to accurately determine their actual current physical position in space or on the surface of the Earth without relying solely on estimated positional calculations, commonly known as dead reckoning. Celestial navigation is performed without using satellite navigation or other similar modern electronic or digital positioning means.
In observational astronomy, culmination is the passage of a celestial object across the observer's local meridian. These events are also known as meridian transits, used in timekeeping and navigation, and measured precisely using a transit telescope.
In the celestial equatorial coordinate system Σ(α, δ) in astronomy, polar distance (PD) is an angular distance of a celestial object on its meridian measured from the celestial pole, similar to the way declination is measured from the celestial equator.
In astronomical navigation, the intercept method, also known as Marcq St. Hilaire method, is a method of calculating an observer's position on Earth (geopositioning). It was originally called the azimuth intercept method because the process involves drawing a line which intercepts the azimuth line. This name was shortened to intercept method and the intercept distance was shortened to 'intercept'.
Longitude by chronometer is a method, in navigation, of determining longitude using a marine chronometer, which was developed by John Harrison during the first half of the eighteenth century. It is an astronomical method of calculating the longitude at which a position line, drawn from a sight by sextant of any celestial body, crosses the observer's assumed latitude. In order to calculate the position line, the time of the sight must be known so that the celestial position i.e. the Greenwich Hour Angle and Declination, of the observed celestial body is known. All that can be derived from a single sight is a single position line, which can be achieved at any time during daylight when both the sea horizon and the sun are visible. To achieve a fix, more than one celestial body and the sea horizon must be visible. This is usually only possible at dawn and dusk.
Ex-meridian is a celestial navigation method of calculating an observer's position on Earth. The method gives the observer a position line on which the observer is situated. It is usually used when the Sun is obscured at noon, and as a result, a meridian altitude is not possible. The navigator measures the altitude of the Sun as close to noon as possible and then calculates where the position line lies.
A lunar standstill or lunistice is when the Moon reaches its furthest north or furthest south point during the course of a month. The declination at lunar standstill varies in a cycle 18.6 years long between 18.134° and 28.725°, due to lunar precession. These extremes are called the minor and major lunar standstills.
The navigational triangle or PZX triangle is a spherical triangle used in astronavigation to determine the observer's position on the globe. It is composed of three reference points on the celestial sphere:
Sun path, sometimes also called day arc, refers to the daily and seasonal arc-like path that the Sun appears to follow across the sky as the Earth rotates and orbits the Sun. The Sun's path affects the length of daytime experienced and amount of daylight received along a certain latitude during a given season.
The position of the Sun in the sky is a function of both the time and the geographic location of observation on Earth's surface. As Earth orbits the Sun over the course of a year, the Sun appears to move with respect to the fixed stars on the celestial sphere, along a circular path called the ecliptic.
The circle of equal altitude, also called circle of position (CoP), is defined as the locus of points on Earth on which an observer sees a celestial object such as the sun or a star, at a given time, with the same observed altitude. It was discovered by the American sea-captain Thomas Hubbard Sumner in 1837, published in 1843 and is the basis of an important method in celestial navigation.