The subsolar point on a planet or a moon is the point at which its Sun is perceived to be directly overhead (at the zenith); [1] that is, where the Sun's rays strike the planet exactly perpendicular to its surface. The subsolar point occurs at the location on a planet or a moon where the Sun culminates at the location's zenith. This occurs at solar noon. At this point, the Sun's rays will fall exactly vertical relative to an object on the ground and thus cast no observable shadow. [2]
Contents
- On Earth
- Coordinates of the subsolar point
- Dates
- Specific observations
- See also
- References
- External links
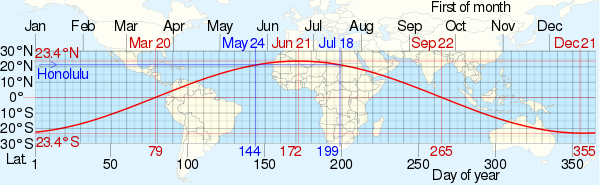
To an observer on a planet with an orientation and rotation similar to those of Earth, the subsolar point will appear to move westward with a speed of 1600 km/h, completing one circuit around the globe each day, approximately moving along the equator. However, it will also move north and south between the tropics over the course of a year, so will appear to spiral like a helix.
The term subsolar point can also mean the point closest to the Sun on an astronomical object, even though the Sun might not be visible.