Merton's portfolio problem

Last updated December 04, 2023

Merton's portfolio problem is a problem in continuous-time finance and in particular intertemporal portfolio choice. An investor must choose how much to consume and must allocate their wealth between stocks and a risk-free asset so as to maximize expected utility. The problem was formulated and solved by Robert C. Merton in 1969 both for finite lifetimes and for the infinite case.^[1]^[2] Research has continued to extend and generalize the model to include factors like transaction costs and bankruptcy.

Problem statement

The investor lives from time 0 to time T; their wealth at time T is denoted W_T. He starts with a known initial wealth W₀ (which may include the present value of wage income). At time t he must choose what amount of his wealth to consume, c_t, and what fraction of wealth to invest in a stock portfolio, π_t (the remaining fraction 1 − π_t being invested in the risk-free asset).

The objective is

\max E\left[\int _{0}^{T}e^{-\rho s}u(c_{s})\,ds+\epsilon ^{\gamma }e^{-\rho T}u(W_{T})\right]

where E is the expectation operator, u is a known utility function (which applies both to consumption and to the terminal wealth, or bequest, W_T), ε parameterizes the desired level of bequest, ρ is the subjective discount rate, and $\gamma$ is a constant which expresses the investor's risk aversion: the higher the gamma, the more reluctance to own stocks.

The wealth evolves according to the stochastic differential equation

dW_{t}=[(r+\pi _{t}(\mu -r))W_{t}-c_{t}]\,dt+W_{t}\pi _{t}\sigma \,dB_{t}

where r is the risk-free rate, (μ, σ) are the expected return and volatility of the stock market and dB_t is the increment of the Wiener process, i.e. the stochastic term of the SDE.

The utility function is of the constant relative risk aversion (CRRA) form:

u(x)={\frac {x^{1-\gamma }}{1-\gamma }}.

Consumption cannot be negative: c_t ≥ 0,^[2]^[3] while π_t is unrestricted (that is borrowing or shorting stocks is allowed).

Investment opportunities are assumed constant, that is r, μ, σ are known and constant, in this (1969) version of the model, although Merton allowed them to change in his intertemporal CAPM (1973).

Solution

Somewhat surprisingly for an optimal control problem, a closed-form solution exists. The optimal consumption and stock allocation depend on wealth and time as follows:^[4]^: 401

\pi (W,t)={\frac {\mu -r}{\sigma ^{2}\gamma }}.

This expression is commonly referred to as Merton's fraction. Because W and t do not appear on the right-hand side; a constant fraction of wealth is invested in stocks, no matter what the age or prosperity of the investor.

c(W,t)={\begin{cases}\nu \left(1+(\nu \epsilon -1)e^{-\nu (T-t)}\right)^{-1}W&{\textrm {if}}\;T<\infty \;{\textrm {and}}\;\nu \neq 0\\(T-t+\epsilon )^{-1}W&{\textrm {if}}\;T<\infty \;{\textrm {and}}\;\nu =0\\\nu W&{\textrm {if}}\;T=\infty \end{cases}}

where $0\leq \epsilon \ll 1$ and

{\begin{aligned}\nu &=\left(\rho -(1-\gamma )\left({\frac {(\mu -r)^{2}}{2\sigma ^{2}\gamma }}+r\right)\right)/\gamma \\&=\rho /\gamma -(1-\gamma )\left({\frac {(\mu -r)^{2}}{2\sigma ^{2}\gamma ^{2}}}+{\frac {r}{\gamma }}\right)\\&=\rho /\gamma -(1-\gamma )(\pi (W,t)^{2}\sigma ^{2}/2+r/\gamma )\\&=\rho /\gamma -(1-\gamma )((\mu -r)\pi (W,t)/2\gamma +r/\gamma ).\end{aligned}}

Extensions

Many variations of the problem have been explored, but most do not lead to a simple closed-form solution.

Flexible retirement age can be taken into account.^[5]
A utility function other than CRRA can be used.
Transaction costs can be introduced.
- For proportional transaction costs the problem was solved by Davis and Norman in 1990.^[6] It is one of the few cases of stochastic singular control where the solution is known. For a graphical representation, the amount invested in each of the two assets can be plotted on the x- and y-axes; three diagonal lines through the origin can be drawn: the upper boundary, the Merton line and the lower boundary. The Merton line represents portfolios having the stock/bond proportion derived by Merton in the absence of transaction costs. As long as the point which represents the current portfolio is near the Merton line, i.e. between the upper and the lower boundary, no action needs to be taken. When the portfolio crosses above the upper or below the lower boundary, one should rebalance the portfolio to bring it back to that boundary. In 1994 Shreve and Soner provided an analysis of the problem via the Hamilton–Jacobi–Bellman equation and its viscosity solutions.^[7]
- When there are fixed transaction costs the problem was addressed by Eastman and Hastings in 1988.^[8] A numerical solution method was provided by Schroder in 1995.^[9]
- Morton and Pliska^[10] considered trading costs that are proportional to the wealth of the investor for logarithmic utility. Although this cost structure seems unrepresentative of real life transaction costs, it can be used to find approximate solutions in cases with additional assets,^[11] for example individual stocks, where it becomes difficult or intractable to give exact solutions for the problem.
The assumption of constant investment opportunities can be relaxed. This requires a model for how $r,\mu ,\sigma$ change over time. An interest rate model could be added and would lead to a portfolio containing bonds of different maturities. Some authors have added a stochastic volatility model of stock market returns.
Bankruptcy can be incorporated. This problem was solved by Karatzas, Lehoczky, Sethi and Shreve in 1986.^[12] Many models incorporating bankruptcy are collected in Sethi (1997).^[13]

Related Research Articles

In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way.

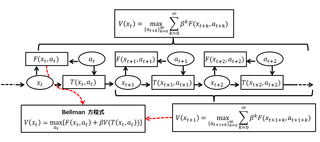
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used.

In theoretical physics, the Rarita–Schwinger equation is the relativistic field equation of spin-3/2 fermions in a four-dimensional flat spacetime. It is similar to the Dirac equation for spin-1/2 fermions. This equation was first introduced by William Rarita and Julian Schwinger in 1941.

When studying and formulating Albert Einstein's theory of general relativity, various mathematical structures and techniques are utilized. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.

In general relativity, the metric tensor is the fundamental object of study. The metric captures all the geometric and causal structure of spacetime, being used to define notions such as time, distance, volume, curvature, angle, and separation of the future and the past.

In mathematical physics, the gamma matrices, $also called the Dirac matrices, are a set of conventional matrices with specific anticommutation relations that ensure they generate a matrix representation of the Clifford algebra It is also possible to define higher-dimensional gamma matrices. When interpreted as the matrices of the action of a set of orthogonal basis vectors for contravariant vectors in Minkowski space, the column vectors on which the matrices act become a space of spinors, on which the Clifford algebra of spacetime acts. This in turn makes it possible to represent infinitesimal spatial rotations and Lorentz boosts. Spinors facilitate spacetime computations in general, and in particular are fundamental to the Dirac equation for relativistic spin particles. Gamma matrices were introduced by Dirac in 1928.$

In physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system. These equations can be viewed as a generalization of the vacuum Maxwell's equations which are normally formulated in the local coordinates of flat spacetime. But because general relativity dictates that the presence of electromagnetic fields induce curvature in spacetime, Maxwell's equations in flat spacetime should be viewed as a convenient approximation.

In the theory of general relativity, a stress–energy–momentum pseudotensor, such as the Landau–Lifshitz pseudotensor, is an extension of the non-gravitational stress–energy tensor that incorporates the energy–momentum of gravity. It allows the energy–momentum of a system of gravitating matter to be defined. In particular it allows the total of matter plus the gravitating energy–momentum to form a conserved current within the framework of general relativity, so that the total energy–momentum crossing the hypersurface of any compact space–time hypervolume vanishes.

In statistics, stochastic volatility models are those in which the variance of a stochastic process is itself randomly distributed. They are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance of the volatility process itself, among others.

The cross-entropy (CE) method is a Monte Carlo method for importance sampling and optimization. It is applicable to both combinatorial and continuous problems, with either a static or noisy objective.

In mathematics and economics, transportation theory or transport theory is a name given to the study of optimal transportation and allocation of resources. The problem was formalized by the French mathematician Gaspard Monge in 1781.

In mathematics, the Wasserstein distance or Kantorovich–Rubinstein metric is a distance function defined between probability distributions on a given metric space $. It is named after Leonid Vaseršteĭn.$

The harmonic coordinate condition is one of several coordinate conditions in general relativity, which make it possible to solve the Einstein field equations. A coordinate system is said to satisfy the harmonic coordinate condition if each of the coordinate functions x^α satisfies d'Alembert's equation. The parallel notion of a harmonic coordinate system in Riemannian geometry is a coordinate system whose coordinate functions satisfy Laplace's equation. Since d'Alembert's equation is the generalization of Laplace's equation to space-time, its solutions are also called "harmonic".

Expected shortfall (ES) is a risk measure—a concept used in the field of financial risk measurement to evaluate the market risk or credit risk of a portfolio. The "expected shortfall at q% level" is the expected return on the portfolio in the worst $of cases. ES is an alternative to value at risk that is more sensitive to the shape of the tail of the loss distribution.$

In mathematical physics, the Dirac algebra is the Clifford algebra $. This was introduced by the mathematical physicist P. A. M. Dirac in 1928 in developing the Dirac equation for spin- 1 / 2 particles with a matrix representation of the gamma matrices, which represent the generators of the algebra.$

Newton–Cartan theory is a geometrical re-formulation, as well as a generalization, of Newtonian gravity first introduced by Élie Cartan and Kurt Friedrichs and later developed by Dautcourt, Dixon, Dombrowski and Horneffer, Ehlers, Havas, Künzle, Lottermoser, Trautman, and others. In this re-formulation, the structural similarities between Newton's theory and Albert Einstein's general theory of relativity are readily seen, and it has been used by Cartan and Friedrichs to give a rigorous formulation of the way in which Newtonian gravity can be seen as a specific limit of general relativity, and by Jürgen Ehlers to extend this correspondence to specific solutions of general relativity.

In mathematical physics, the Dirac equation in curved spacetime is a generalization of the Dirac equation from flat spacetime to curved spacetime, a general Lorentzian manifold.

Stochastic portfolio theory (SPT) is a mathematical theory for analyzing stock market structure and portfolio behavior introduced by E. Robert Fernholz in 2002. It is descriptive as opposed to normative, and is consistent with the observed behavior of actual markets. Normative assumptions, which serve as a basis for earlier theories like modern portfolio theory (MPT) and the capital asset pricing model (CAPM), are absent from SPT.

In general relativity and tensor calculus, the Palatini identity is

In mathematical physics, the Gordon decomposition of the Dirac current is a splitting of the charge or particle-number current into a part that arises from the motion of the center of mass of the particles and a part that arises from gradients of the spin density. It makes explicit use of the Dirac equation and so it applies only to "on-shell" solutions of the Dirac equation.

References

↑ Merton, R. C. (1 August 1969). "Lifetime Portfolio Selection under Uncertainty: the Continuous-Time Case". The Review of Economics and Statistics. 51 (3): 247–257. doi:10.2307/1926560. ISSN 0034-6535. JSTOR 1926560.
1 2 Sethi, S.P. and Taksar, M.I., “A Note on Merton's 'Optimum Consumption and Portfolio Rules in a Continuous-Time Model,” Journal of Economic Theory, 46, 1988, 395-401.
↑ Karatzas, Ioannis; Lehoczky, John P.; Sethi, Suresh P.; Shreve, Steven E. (May 1986). "Explicit Solution of a General Consumption/Investment Problem". Mathematics of Operations Research . 11 (2): 261–294. doi:10.1287/moor.11.2.261.
↑ Merton, R. C. (1971). "Optimum consumption and portfolio rules in a continuous-time model" (PDF). Journal of Economic Theory. 3 (4): 373–413. doi:10.1016/0022-0531(71)90038-X. hdl: 1721.1/63980 .
↑ Bodie, Z.; Merton, R. C.; Samuelson, W. F. (1992). "Labor supply flexibility and portfolio choice in a life cycle model" (PDF). Journal of Economic Dynamics and Control. 16 (3–4): 427. doi:10.1016/0165-1889(92)90044-F. S2CID 16699153.
↑ Davis, M. H. A.; Norman, A. R. (1990). "Portfolio Selection with Transaction Costs" (PDF). Mathematics of Operations Research . 15 (4): 676. doi:10.1287/moor.15.4.676. hdl:10044/1/11848. JSTOR 3689770.
↑ Shreve, S. E.; Soner, H. M. (1994). "Optimal Investment and Consumption with Transaction Costs". The Annals of Applied Probability. 4 (3): 609. doi: 10.1214/aoap/1177004966 . JSTOR 2245058.
↑ Eastham, Jerome F.; Hastings, Kevin J. (1988). "Optimal Impulse Control of Portfolios". Mathematics of Operations Research . 13 (4): 588. doi:10.1287/moor.13.4.588. JSTOR 3689945.
↑ Schroder, M. (1995). "Optimal Portfolio Selection with Fixed Transaction Costs: Numerical Solutions" (PDF). Working Paper. Michigan State University.
↑ Morton, A. J.; Pliska, S. R. (1995). "Optimal Portfolio Management with Fixed Transaction Costs". Mathematical Finance. 5 (4): 337. doi:10.1111/j.1467-9965.1995.tb00071.x.
↑ "Archived copy" (PDF). Archived from the original (PDF) on 2014-11-08. Retrieved 2014-10-28.{{cite web}}: CS1 maint: archived copy as title (link)
↑ Karatzas, I.; Lehoczky, J. P.; Sethi, S. P.; Shreve, S. E. (1985). "Explicit solution of a general consumption/investment problem". Stochastic Differential Systems. Lecture Notes in Control and Information Sciences. Vol. 78. p. 209. doi:10.1007/BFb0041165. ISBN 3-540-16228-3.
↑ Sethi, S. P. (1997). Optimal Consumption and Investment with Bankruptcy. doi:10.1007/978-1-4615-6257-3. ISBN 978-1-4613-7871-6.