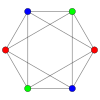
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and , that is, every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In graph theory, an independent set, stable set, coclique or anticlique is a set of vertices in a graph, no two of which are adjacent. That is, it is a set of vertices such that for every two vertices in , there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in . A set is independent if and only if it is a clique in the graph's complement. The size of an independent set is the number of vertices it contains. Independent sets have also been called "internally stable sets", of which "stable set" is a shortening.

In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.
In the mathematical discipline of graph theory, a matching or independent edge set in an undirected graph is a set of edges without common vertices. In other words, a subset of the edges is a matching if each vertex appears in at most one edge of that matching. Finding a matching in a bipartite graph can be treated as a network flow problem.

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In graph theory, a complete coloring is a (proper) vertex coloring in which every pair of colors appears on at least one pair of adjacent vertices. Equivalently, a complete coloring is minimal in the sense that it cannot be transformed into a proper coloring with fewer colors by merging pairs of color classes. The achromatic numberψ(G) of a graph G is the maximum number of colors possible in any complete coloring of G.

In graph theory, a dominating set for a graph G is a subset D of its vertices, such that any vertex of G is in D, or has a neighbor in D. The domination numberγ(G) is the number of vertices in a smallest dominating set for G.
In graph theory, a domatic partition of a graph is a partition of into disjoint sets , ,..., such that each Vi is a dominating set for G. The figure on the right shows a domatic partition of a graph; here the dominating set consists of the yellow vertices, consists of the green vertices, and consists of the blue vertices.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In graph theory, the Grundy number or Grundy chromatic number of an undirected graph is the maximum number of colors that can be used by a greedy coloring strategy that considers the vertices of the graph in sequence and assigns each vertex its first available color, using a vertex ordering chosen to use as many colors as possible. Grundy numbers are named after P. M. Grundy, who studied an analogous concept for directed graphs in 1939. The undirected version was introduced by Christen & Selkow (1979).

In graph theory, boxicity is a graph invariant, introduced by Fred S. Roberts in 1969.
In the mathematical fields of graph theory and combinatorial optimization, the bipartite dimension or biclique cover number of a graph G = (V, E) is the minimum number of bicliques (that is complete bipartite subgraphs), needed to cover all edges in E. A collection of bicliques covering all edges in G is called a biclique edge cover, or sometimes biclique cover. The bipartite dimension of G is often denoted by the symbol d(G).

In the mathematical discipline of graph theory, a 3-dimensional matching is a generalization of bipartite matching to 3-partite hypergraphs, which consist of hyperedges each of which contains 3 vertices.

In graph theory, a well-covered graph is an undirected graph in which the minimal vertex covers all have the same size. Here, a vertex cover is a set of vertices that touches all edges, and it is minimal if removing any vertex from it would leave some edge uncovered. Equivalently, well-covered graphs are the graphs in which all maximal independent sets have equal size. Well-covered graphs were defined and first studied by Michael D. Plummer in 1970.
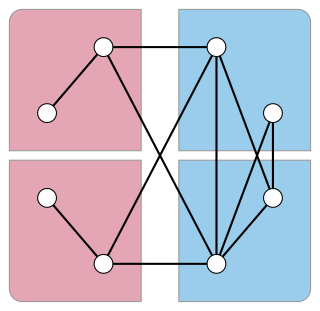
In graph theory, a skew partition of a graph is a partition of its vertices into two subsets, such that the induced subgraph formed by one of the two subsets is disconnected and the induced subgraph formed by the other subset is the complement of a disconnected graph. Skew partitions play an important role in the theory of perfect graphs.

In graph theory, a split of an undirected graph is a cut whose cut-set forms a complete bipartite graph. A graph is prime if it has no splits. The splits of a graph can be collected into a tree-like structure called the split decomposition or join decomposition, which can be constructed in linear time. This decomposition has been used for fast recognition of circle graphs and distance-hereditary graphs, as well as for other problems in graph algorithms.
In graph theory, the term bipartite hypergraph describes several related classes of hypergraphs, all of which are natural generalizations of a bipartite graph.