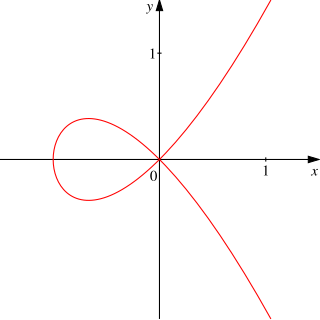Ceva's theorem is a theorem about triangles in plane geometry. Given a triangle ABC, let the lines AO, BO and CO be drawn from the vertices to a common point O, to meet opposite sides at D, E and F respectively. Then, using signed lengths of segments,

In geometry, a pedal triangle is obtained by projecting a point onto the sides of a triangle.

In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral. It is a central line of the triangle, and it passes through several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the nine-point circle of the triangle.

In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.

In geometry, a set of points are said to be concyclic if they lie on a common circle. All concyclic points are at the same distance from the center of the circle. Three points in the plane that do not all fall on a straight line are concyclic, but four or more such points in the plane are not necessarily concyclic.

In the geometry of triangles, the incircle and nine-point circle of a triangle are internally tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is a triangle center, meaning that its definition does not depend on the placement and scale of the triangle. It is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers, and is named after Karl Wilhelm Feuerbach.
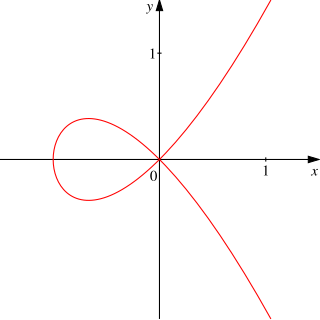
In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equation
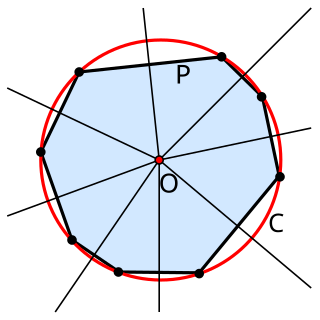
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.

In geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the total distance from the three vertices of the triangle to the point is the minimum possible. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it.
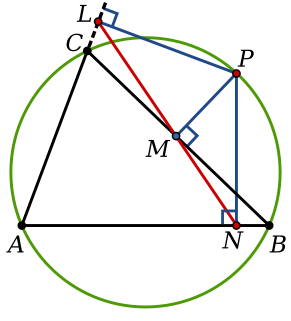
In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. The line through these points is the Simson line of P, named for Robert Simson. The concept was first published, however, by William Wallace in 1799.
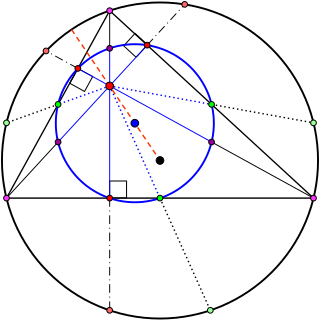
In geometry, the nine-point center is a triangle center, a point defined from a given triangle in a way that does not depend on the placement or scale of the triangle. It is so called because it is the center of the nine-point circle, a circle that passes through nine significant points of the triangle: the midpoints of the three edges, the feet of the three altitudes, and the points halfway between the orthocenter and each of the three vertices. The nine-point center is listed as point X(5) in Clark Kimberling's Encyclopedia of Triangle Centers.

In Euclidean geometry, the isodynamic points of a triangle are points associated with the triangle, with the properties that an inversion centered at one of these points transforms the given triangle into an equilateral triangle, and that the distances from the isodynamic point to the triangle vertices are inversely proportional to the opposite side lengths of the triangle. Triangles that are similar to each other have isodynamic points in corresponding locations in the plane, so the isodynamic points are triangle centers, and unlike other triangle centers the isodynamic points are also invariant under Möbius transformations. A triangle that is itself equilateral has a unique isodynamic point, at its centroid; every non-equilateral triangle has two isodynamic points. Isodynamic points were first studied and named by Joseph Neuberg (1885).

In geometry, a set of Johnson circles comprises three circles of equal radius r sharing one common point of intersection H. In such a configuration the circles usually have a total of four intersections : the common point H that they all share, and for each of the three pairs of circles one more intersection point. If any two of the circles happen to osculate, they only have H as a common point, and it will then be considered that H be their 2-wise intersection as well; if they should coincide we declare their 2-wise intersection be the point diametrically opposite H. The three 2-wise intersection points define the reference triangle of the figure. The concept is named after Roger Arthur Johnson.

In geometry, the de Longchamps point of a triangle is a triangle center named after French mathematician Gaston Albert Gohierre de Longchamps. It is the reflection of the orthocenter of the triangle about the circumcenter.
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.

In Euclidean geometry, Kosnita's theorem is a property of certain circles associated with an arbitrary triangle.

In Euclidean geometry, the Droz-Farny line theorem is a property of two perpendicular lines through the orthocenter of an arbitrary triangle.
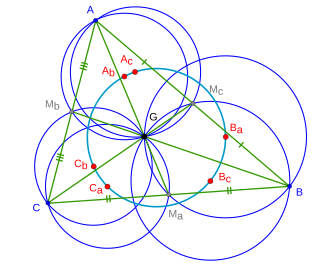
In Euclidean plane geometry, the van Lamoen circle is a special circle associated with any given triangle . It contains the circumcenters of the six triangles that are defined inside by its three medians.
In geometry, the circumcenter of mass is a center associated with a polygon which shares many of the properties of the center of mass. More generally, the circumcenter of mass may be defined for simplicial polytopes and also in the spherical and hyperbolic geometries.