
Sir John Anthony Pople was a British theoretical chemist who was awarded the Nobel Prize in Chemistry with Walter Kohn in 1998 for his development of computational methods in quantum chemistry.
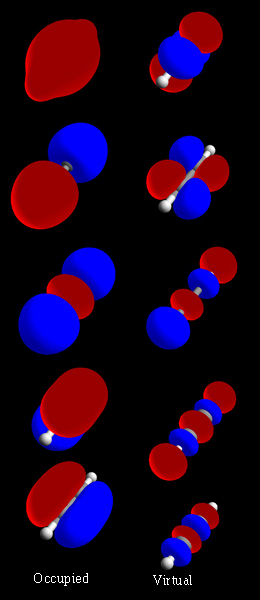
In chemistry, a molecular orbital is a mathematical function describing the location and wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The terms atomic orbital and molecular orbital were introduced by Robert S. Mulliken in 1932 to mean one-electron orbital wave functions. At an elementary level, they are used to describe the region of space in which a function has a significant amplitude.
Slater-type orbitals (STOs) are functions used as atomic orbitals in the linear combination of atomic orbitals molecular orbital method. They are named after the physicist John C. Slater, who introduced them in 1930.
In computational chemistry and molecular physics, Gaussian orbitals are functions used as atomic orbitals in the LCAO method for the representation of electron orbitals in molecules and numerous properties that depend on these.
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state.
In molecular physics, the Pariser–Parr–Pople method applies semi-empirical quantum mechanical methods to the quantitative prediction of electronic structures and spectra, in molecules of interest in the field of organic chemistry. Previous methods existed—such as the Hückel method which led to Hückel's rule—but were limited in their scope, application and complexity, as is the Extended Hückel method.
The extended Hückel method is a semiempirical quantum chemistry method, developed by Roald Hoffmann since 1963. It is based on the Hückel method but, while the original Hückel method only considers pi orbitals, the extended method also includes the sigma orbitals.
Møller–Plesset perturbation theory (MP) is one of several quantum chemistry post-Hartree–Fock ab initio methods in the field of computational chemistry. It improves on the Hartree–Fock method by adding electron correlation effects by means of Rayleigh–Schrödinger perturbation theory (RS-PT), usually to second (MP2), third (MP3) or fourth (MP4) order. Its main idea was published as early as 1934 by Christian Møller and Milton S. Plesset.
In theoretical and computational chemistry, a basis set is a set of functions that is used to represent the electronic wave function in the Hartree–Fock method or density-functional theory in order to turn the partial differential equations of the model into algebraic equations suitable for efficient implementation on a computer.
Koopmans' theorem states that in closed-shell Hartree–Fock theory (HF), the first ionization energy of a molecular system is equal to the negative of the orbital energy of the highest occupied molecular orbital (HOMO). This theorem is named after Tjalling Koopmans, who published this result in 1934.
MNDO, or Modified Neglect of Diatomic Overlap is a semi-empirical method for the quantum calculation of molecular electronic structure in computational chemistry. It is based on the Neglect of Diatomic Differential Overlap integral approximation. Similarly, this method replaced the earlier MINDO method. It is part of the MOPAC program and was developed in the group of Michael Dewar. It is also part of the AMPAC, GAMESS (US), PC GAMESS, GAMESS (UK), Gaussian, ORCA and CP2K programs.

PM3, or Parametric Method 3, is a semi-empirical method for the quantum calculation of molecular electronic structure in computational chemistry. It is based on the Neglect of Differential Diatomic Overlap integral approximation.
Complete Neglect of Differential Overlap (CNDO) is one of the first semi empirical methods in quantum chemistry. It uses the core approximation, in which only the outer valence electrons are explicitly included, and the approximation of zero-differential overlap.
The Hückel method or Hückel molecular orbital theory, proposed by Erich Hückel in 1930, is a simple method for calculating molecular orbitals as linear combinations of atomic orbitals. The theory predicts the molecular orbitals for π-electrons in π-delocalized molecules, such as ethylene, benzene, butadiene, and pyridine. It provides the theoretical basis for Hückel's rule that cyclic, planar molecules or ions with π-electrons are aromatic. It was later extended to conjugated molecules such as pyridine, pyrrole and furan that contain atoms other than carbon and hydrogen (heteroatoms). A more dramatic extension of the method to include σ-electrons, known as the extended Hückel method (EHM), was developed by Roald Hoffmann. The extended Hückel method gives some degree of quantitative accuracy for organic molecules in general and was used to provide computational justification for the Woodward–Hoffmann rules. To distinguish the original approach from Hoffmann's extension, the Hückel method is also known as the simple Hückel method (SHM).
INDO stands for Intermediate Neglect of Differential Overlap. It is a semi-empirical quantum chemistry method that is a development of the complete neglect of differential overlap (CNDO/2) method introduced by John Pople. Like CNDO/2 it uses zero-differential overlap for the two-electron integrals but not for integrals that are over orbitals centered on the same atom.
Unrestricted Hartree–Fock (UHF) theory is the most common molecular orbital method for open shell molecules where the number of electrons of each spin are not equal. While restricted Hartree–Fock theory uses a single molecular orbital twice, one multiplied by the α spin function and the other multiplied by the β spin function in the Slater determinant, unrestricted Hartree–Fock theory uses different molecular orbitals for the α and β electrons. This has been called a different orbitals for different spins (DODS) method. The result is a pair of coupled Roothaan equations, known as the Pople–Nesbet–Berthier equations.
Zero differential overlap is an approximation in computational molecular orbital theory that is the central technique of semi-empirical methods in quantum chemistry. When computers were first used to calculate bonding in molecules, it was only possible to calculate diatomic molecules. As computers advanced, it became possible to study larger molecules, but the use of this approximation has always allowed the study of even larger molecules. Currently semi-empirical methods can be applied to molecules as large as whole proteins. The approximation involves ignoring certain integrals, usually two-electron repulsion integrals. If the number of orbitals used in the calculation is N, the number of two-electron repulsion integrals scales as N4. After the approximation is applied the number of such integrals scales as N2, a much smaller number, simplifying the calculation.
Semi-empirical quantum chemistry methods are based on the Hartree–Fock formalism, but make many approximations and obtain some parameters from empirical data. They are very important in computational chemistry for treating large molecules where the full Hartree–Fock method without the approximations is too expensive. The use of empirical parameters appears to allow some inclusion of electron correlation effects into the methods.

COSMO is a calculation method for determining the electrostatic interaction of a molecule with a solvent. COSMO is a dielectric continuum model. These models can be used in computational chemistry to model solvation effects. COSMO has become a popular method of these solvation models in recent years. The COSMO formalism is similar to the method proposed earlier by Hoshi et al. The COSMO approach is based - as many other dielectric continuum models - on the surface segmentation of a molecule surface.
SAM1, or "Semiempirical ab initio Model 1", is a semiempirical quantum chemistry method for computing molecular properties. It is an implementation the general Neglect of Differential Diatomic Overlap (NDDO) integral approximation, and is efficient and accurate. Related methods are AM1, PM3 and the older MNDO.





