Newton-Hooke priority controversy for the inverse square law

Last updated

In 1686, [lower-alpha 1] when the first book of Newton's Principia was presented to the Royal Society, Robert Hooke accused Newton of plagiarism by claiming that he had taken from him the "notion" of "the rule of the decrease of Gravity, being reciprocally as the squares of the distances from the Center". At the same time (according to Edmond Halley's contemporary report) Hooke agreed that "the Demonstration of the Curves generated thereby" was wholly Newton's. [1]

Contents

A modern assessment of the early history of the inverse square law is that "by the late 1670s", the assumption of an "inverse proportion between gravity and the square of distance was rather common and had been advanced by a number of different people for different reasons". [2] The same author credits Robert Hooke with a significant and seminal contribution, but treats Hooke's claim of priority on the inverse square point as irrelevant, as several individuals besides Newton and Hooke had suggested it. He points instead to the idea of "compounding the celestial motions" and the conversion of Newton's thinking away from "centrifugal" and towards "centripetal" force as Hooke's significant contributions.

Newton gave credit in his Principia to two people: Bullialdus (who wrote without proof that there was a force on the Earth towards the Sun), and Borelli (who wrote that all planets were attracted towards the Sun). [3] [4] The main influence may have been Borelli, whose book Newton had a copy of. [5]

Hooke's work and claims

Robert Hooke published his ideas about the "System of the World" in the 1660s, when he read to the Royal Society on March 21, 1666, a paper "concerning the inflection of a direct motion into a curve by a supervening attractive principle", and he published them again in somewhat developed form in 1674, as an addition to "An Attempt to Prove the Motion of the Earth from Observations". [6] Hooke announced in 1674 that he planned to "explain a System of the World differing in many particulars from any yet known", based on three suppositions: that "all Celestial Bodies whatsoever, have an attraction or gravitating power towards their own Centers" and "also attract all the other Celestial Bodies that are within the sphere of their activity"; [7] that "all bodies whatsoever that are put into a direct and simple motion, will so continue to move forward in a straight line, till they are by some other effectual powers deflected and bent..." and that "these attractive powers are so much the more powerful in operating, by how much the nearer the body wrought upon is to their own Centers". Thus Hooke postulated mutual attractions between the Sun and planets, in a way that increased with nearness to the attracting body, together with a principle of linear inertia.

Hooke's statements up to 1674 made no mention, however, that an inverse square law applies or might apply to these attractions. Hooke's gravitation was also not yet universal, though it approached universality more closely than previous hypotheses. [8] He also did not provide accompanying evidence or mathematical demonstration. On the latter two aspects, Hooke himself stated in 1674: "Now what these several degrees [of attraction] are I have not yet experimentally verified"; and as to his whole proposal: "This I only hint at present", "having my self many other things in hand which I would first compleat, and therefore cannot so well attend it" (i.e. "prosecuting this Inquiry"). [6] It was later on, in writing on 6 January 1680 to Newton, that Hooke communicated his "supposition ... that the Attraction always is in a duplicate proportion to the Distance from the Center Reciprocall, and Consequently that the Velocity will be in a subduplicate proportion to the Attraction and Consequently as Kepler Supposes Reciprocall to the Distance." [9] (The inference about the velocity was incorrect.) [10]

Hooke's correspondence with Newton during 1679–1680 not only mentioned this inverse square supposition for the decline of attraction with increasing distance, but also, in Hooke's opening letter to Newton, of 24 November 1679, an approach of "compounding the celestial motions of the planets of a direct motion by the tangent & an attractive motion towards the central body". [11]

Newton's work and claims

Newton, faced in May 1686 with Hooke's claim on the inverse square law, denied that Hooke was to be credited as author of the idea. Among the reasons, Newton recalled that the idea had been discussed with Sir Christopher Wren previous to Hooke's 1679 letter. [12] Newton also pointed out and acknowledged prior work of others, [13] including Bullialdus, [3] (who suggested, but without demonstration, that there was an attractive force from the Sun in the inverse square proportion to the distance), and Borelli [4] (who suggested, also without demonstration, that there was a centrifugal tendency in counterbalance with a gravitational attraction towards the Sun so as to make the planets move in ellipses). D T Whiteside has described the contribution to Newton's thinking that came from Borelli's book, a copy of which was in Newton's library at his death. [5]

Newton further defended his work by saying that had he first heard of the inverse square proportion from Hooke, he would still have some rights to it in view of his demonstrations of its accuracy. Hooke, without evidence in favor of the supposition, could only guess that the inverse square law was approximately valid at great distances from the center. According to Newton, while the 'Principia' was still at pre-publication stage, there were so many a priori reasons to doubt the accuracy of the inverse-square law (especially close to an attracting sphere) that "without my (Newton's) Demonstrations, to which Mr Hooke is yet a stranger, it cannot believed by a judicious Philosopher to be any where accurate." [14]

This remark refers among other things to Newton's finding, supported by mathematical demonstration, that if the inverse square law applies to tiny particles, then even a large spherically symmetrical mass also attracts masses external to its surface, even close up, exactly as if all its own mass were concentrated at its center. Thus Newton gave a justification, otherwise lacking, for applying the inverse square law to large spherical planetary masses as if they were tiny particles. [15] In addition, Newton had formulated, in Propositions 43–45 of Book 1 [16] and associated sections of Book 3, a sensitive test of the accuracy of the inverse square law, in which he showed that only where the law of force is calculated as the inverse square of the distance will the directions of orientation of the planets' orbital ellipses stay constant as they are observed to do apart from small effects attributable to inter-planetary perturbations.

In regard to evidence that still survives of the earlier history, manuscripts written by Newton in the 1660s show that Newton himself had, by 1669, arrived at proofs that in a circular case of planetary motion, "endeavour to recede" (what was later called centrifugal force) had an inverse-square relation with distance from the center. [17] After his 1679–1680 correspondence with Hooke, Newton adopted the language of inward or centripetal force. According to Newton scholar J. Bruce Brackenridge, although much has been made of the change in language and difference of point of view, as between centrifugal or centripetal forces, the actual computations and proofs remained the same either way. They also involved the combination of tangential and radial displacements, which Newton was making in the 1660s. The lesson offered by Hooke to Newton here, although significant, was one of perspective and did not change the analysis. [18] This background shows there was basis for Newton to deny deriving the inverse square law from Hooke.

Newton's acknowledgment

On the other hand, Newton did accept and acknowledge, in all editions of the Principia, that Hooke (but not exclusively Hooke) had separately appreciated the inverse square law in the solar system. Newton acknowledged Wren, Hooke, and Halley in this connection in the Scholium to Proposition 4 in Book 1. [19] Newton also acknowledged to Halley that his correspondence with Hooke in 1679–80 had reawakened his dormant interest in astronomical matters, but that did not mean, according to Newton, that Hooke had told Newton anything new or original: "yet am I not beholden to him for any light into that business but only for the diversion he gave me from my other studies to think on these things & for his dogmaticalness in writing as if he had found the motion in the Ellipsis, which inclined me to try it ..." [13]

Modern priority controversy

Since the time of Newton and Hooke, scholarly discussion has also touched on the question of whether Hooke's 1679 mention of 'compounding the motions' provided Newton with something new and valuable, even though that was not a claim actually voiced by Hooke at the time. As described above, Newton's manuscripts of the 1660s do show him actually combining tangential motion with the effects of radially directed force or endeavour, for example in his derivation of the inverse square relation for the circular case. They also show Newton clearly expressing the concept of linear inertia—for which he was indebted to Descartes' work, published in 1644 (as Hooke probably was). [20] These matters do not appear to have been learned by Newton from Hooke.

Nevertheless, a number of authors have had more to say about what Newton gained from Hooke and some aspects remain controversial. [21] [22] [23] The fact that most of Hooke's private papers had been destroyed or have disappeared does not help to establish the truth.

Newton's role in relation to the inverse square law was not as it has sometimes been represented. He did not claim to think it up as a bare idea. What Newton did, was to show how the inverse-square law of attraction had many necessary mathematical connections with observable features of the motions of bodies in the solar system; and that they were related in such a way that the observational evidence and the mathematical demonstrations, taken together, gave reason to believe that the inverse square law was not just approximately true but exactly true (to the accuracy achievable in Newton's time and for about two centuries afterwards – and with some loose ends of points that could not yet be certainly examined, where the implications of the theory had not yet been adequately identified or calculated). [24] [25]

Regardless of claims, Newton's refined inverse square law completely superseded all previous attempts at inverse square relationships, and despite giving credit to Wren, Hooke, and Halley, could have cited his own work from 1666. [26] Also made clear is that Hooke's work not only lacked mathematical rigor, but was also physically wrong in its applications. [26]

About thirty years after Newton's death in 1727, Alexis Clairaut, a mathematical astronomer eminent in his own right in the field of gravitational studies, wrote after reviewing what Hooke published, that "One must not think that this idea ... of Hooke diminishes Newton's glory"; and that "the example of Hooke" serves "to show what a distance there is between a truth that is glimpsed and a truth that is demonstrated". [27] [28]

Notes

  1. ↑ Dates in this article are given according to the Julian calendar, which was still in use in England at the time. Dates of events between 1 January and 24 March inclusive have an additional complication: formally the civil year began on 25 March although common practice then as now was to start the year on 1 January. Wikipedia follows the convention adopted by most modern historical writing of retaining the dates according to the Julian calendar but taking the year as starting on 1 January rather than 25 March. Some sources use the notation 16⁠85/86⁠ for dates in January, February and March, to indicate both the legal year was still 1685 but the common year had advanced to 1686. For a more detailed explanation, see dual dating and Calendar (New Style) Act 1750.)

Related Research Articles

<span class="mw-page-title-main">Isaac Newton</span> English mathematician and physicist

Sir Isaac Newton was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author who was described in his time as a natural philosopher. He was a key figure in the Scientific Revolution and the Enlightenment that followed. His pioneering book Philosophiæ Naturalis Principia Mathematica, first published in 1687, consolidated many previous results and established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for formulating infinitesimal calculus, though he developed calculus years before Leibniz.

<span class="mw-page-title-main">Kepler's laws of planetary motion</span>

In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:

  1. The orbit of a planet is an ellipse with the Sun at one of the two foci.
  2. A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
  3. The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.
<span class="mw-page-title-main">Mass</span> Amount of matter present in an object

Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies.

<span class="mw-page-title-main">Scientific Revolution</span> Emergence of modern science in the early modern period

The Scientific Revolution was a series of events that marked the emergence of modern science during the early modern period, when developments in mathematics, physics, astronomy, biology and chemistry transformed the views of society about nature. The Scientific Revolution took place in Europe in the second half of the Renaissance period, with the 1543 Nicolaus Copernicus publication De revolutionibus orbium coelestium often cited as its beginning.

<span class="mw-page-title-main">Gravity</span> Attraction of masses and energy

In physics, gravity (from Latin gravitas 'weight') is a fundamental interaction primarily observed as mutual attraction between all things that have mass. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the strong interaction, 1036 times weaker than the electromagnetic force and 1029 times weaker than the weak interaction. As a result, it has no significant influence at the level of subatomic particles. However, gravity is the most significant interaction between objects at the macroscopic scale, and it determines the motion of planets, stars, galaxies, and even light.

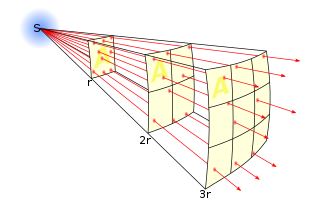
<span class="mw-page-title-main">Inverse-square law</span> Physical law

In science, an inverse-square law is any scientific law stating that the observed "intensity" of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cause for this can be understood as geometric dilution corresponding to point-source radiation into three-dimensional space.

<i>Philosophiæ Naturalis Principia Mathematica</i> 1687 work by Isaac Newton

Philosophiæ Naturalis Principia Mathematica often referred to as simply the Principia, is a book by Isaac Newton that expounds Newton's laws of motion and his law of universal gravitation. The Principia is written in Latin and comprises three volumes, and was authorized, imprimatur, by Samuel Pepys, then-President of the Royal Society on 5 July 1686 and first published in 1687.

<span class="mw-page-title-main">Robert Hooke</span> English scientist, architect, polymath (1635–1703)

Robert Hooke was an English polymath who was active as a physicist, astronomer, geologist, meteorologist and architect. He is credited as one of the first scientists to investigate living things at microscopic scale in 1665, using a compound microscope that he designed. Hooke was an impoverished scientific inquirer in young adulthood who went on to become one of the most important scientists of his time. After the Great Fire of London in 1666, Hooke attained wealth and esteem by performing more than half of the property line surveys and assisting with the city's rapid reconstruction. Often vilified by writers in the centuries after his death, his reputation was restored at the end of the twentieth century and he has been called "England's Leonardo [da Vinci]".

The following is a timeline of classical mechanics:

Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics to astronomical objects, such as stars and planets, to produce ephemeris data.

<span class="mw-page-title-main">Alexis Clairaut</span> French mathematician, astronomer, and geophysicist (1713–1765)

Alexis Claude Clairaut was a French mathematician, astronomer, and geophysicist. He was a prominent Newtonian whose work helped to establish the validity of the principles and results that Sir Isaac Newton had outlined in the Principia of 1687. Clairaut was one of the key figures in the expedition to Lapland that helped to confirm Newton's theory for the figure of the Earth. In that context, Clairaut worked out a mathematical result now known as "Clairaut's theorem". He also tackled the gravitational three-body problem, being the first to obtain a satisfactory result for the apsidal precession of the Moon's orbit. In mathematics he is also credited with Clairaut's equation and Clairaut's relation.

Newton's law of universal gravitation says that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Separated objects attract and are attracted as if all their mass were concentrated at their centers. The publication of the law has become known as the "first great unification", as it marked the unification of the previously described phenomena of gravity on Earth with known astronomical behaviors.

<span class="mw-page-title-main">Early life of Isaac Newton</span>

The following article is part of a biography of Sir Isaac Newton, the English mathematician and scientist, author of the Principia. It portrays the years after Newton's birth in 1642, his education, as well as his early scientific contributions, before the writing of his main work, the Principia Mathematica, in 1685.

De motu corporum in gyrum is the presumed title of a manuscript by Isaac Newton sent to Edmond Halley in November 1684. The manuscript was prompted by a visit from Halley earlier that year when he had questioned Newton about problems then occupying the minds of Halley and his scientific circle in London, including Sir Christopher Wren and Robert Hooke.

Lunar theory attempts to account for the motions of the Moon. There are many small variations in the Moon's motion, and many attempts have been made to account for them. After centuries of being problematic, lunar motion can now be modeled to a very high degree of accuracy.

<span class="mw-page-title-main">Leibniz–Newton calculus controversy</span> Public dispute between Isaac Newton and Gottfried Leibniz (beginning 1699)

In the history of calculus, the calculus controversy was an argument between the mathematicians Isaac Newton and Gottfried Wilhelm Leibniz over who had first invented calculus. The question was a major intellectual controversy, which began simmering in 1699 and broke out in full force in 1711. Leibniz had published his work first, but Newton's supporters accused Leibniz of plagiarizing Newton's unpublished ideas. Leibniz died in 1716, shortly after the Royal Society, of which Newton was a member, found in Newton's favor. The modern consensus is that the two men developed their ideas independently.

<span class="mw-page-title-main">History of gravitational theory</span>

In physics, theories of gravitation postulate mechanisms of interaction governing the movements of bodies with mass. There have been numerous theories of gravitation since ancient times. The first extant sources discussing such theories are found in ancient Greek philosophy. This work was furthered through the Middle Ages by Indian, Islamic, and European scientists, before gaining great strides during the Renaissance and Scientific Revolution—culminating in the formulation of Newton's law of gravity. This was superseded by Albert Einstein's theory of relativity in the early 20th century.

Mechanical explanations of gravitation are attempts to explain the action of gravity by aid of basic mechanical processes, such as pressure forces caused by pushes, without the use of any action at a distance. These theories were developed from the 16th until the 19th century in connection with the aether. However, such models are no longer regarded as viable theories within the mainstream scientific community and general relativity is now the standard model to describe gravitation without the use of actions at a distance. Modern "quantum gravity" hypotheses also attempt to describe gravity by more fundamental processes such as particle fields, but they are not based on classical mechanics.

<span class="mw-page-title-main">Newton's theorem of revolving orbits</span> Theorem in classical mechanics

In classical mechanics, Newton's theorem of revolving orbits identifies the type of central force needed to multiply the angular speed of a particle by a factor k without affecting its radial motion. Newton applied his theorem to understanding the overall rotation of orbits that is observed for the Moon and planets. The term "radial motion" signifies the motion towards or away from the center of force, whereas the angular motion is perpendicular to the radial motion.

<span class="mw-page-title-main">Edmond Halley</span> English astronomer (1656–1742)

EdmondHalley was an English astronomer, mathematician and physicist. He was the second Astronomer Royal in Britain, succeeding John Flamsteed in 1720.

References

  1. ↑ H W Turnbull (ed.), Correspondence of Isaac Newton, Vol 2 (1676–1687), (Cambridge University Press, 1960), giving the Halley–Newton correspondence of May to July 1686 about Hooke's claims at pp. 431–448, see particularly page 431.
  2. ↑ Discussion points can be seen for example in the following papers:
    • Guicciardini, Niccolò (2005). "Reconsidering the Hooke–Newton Debate on Gravitation: Recent Results". Early Science and Medicine. 10 (4): 510–517. doi:10.1163/157338205774661825. JSTOR   4130420.
    • Gal, Ofer (2005). "The Invention of Celestial Mechanics". Early Science and Medicine. 10 (4): 529–534. doi:10.1163/157338205774661834. JSTOR   4130422.
    • Nauenberg, M. (2005). "Hooke's and Newton's Contributions to the Early Development of Orbital mechanics and Universal Gravitation". Early Science and Medicine. 10 (4): 518–528. doi:10.1163/157338205774661861. JSTOR   4130421.
  3. 1 2 Bullialdus (Ismael Bouillau) (1645), "Astronomia philolaica", Paris, 1645.
  4. 1 2 Borelli, G. A., "Theoricae Mediceorum Planetarum ex causis physicis deductae", Florence, 1666.
  5. 1 2 See especially p. 13 in Whiteside, D. T. (1970). "Before the Principia: The Maturing of Newton's Thoughts on Dynamical Astronomy, 1664–1684". Journal for the History of Astronomy. 1: 5–19. Bibcode:1970JHA.....1....5W. doi:10.1177/002182867000100103. S2CID   125845242.
  6. 1 2 Hooke's 1674 statement in "An Attempt to Prove the Motion of the Earth from Observations" is available in online facsimile here.
  7. ↑ Purrington, Robert D. (2009). The First Professional Scientist: Robert Hooke and the Royal Society of London. Springer. p. 168. ISBN   978-3-0346-0036-1. Extract of page 168
  8. ↑ See page 239 in Curtis Wilson (1989), "The Newtonian achievement in astronomy", ch.13 (pages 233–274) in "Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton", CUP 1989.
  9. ↑ Page 309 in H W Turnbull (ed.), Correspondence of Isaac Newton, Vol 2 (1676–1687), (Cambridge University Press, 1960), document #239.
  10. ↑ See Curtis Wilson (1989) at page 244.
  11. ↑ Page 297 in H W Turnbull (ed.), Correspondence of Isaac Newton, Vol 2 (1676–1687), (Cambridge University Press, 1960), document #235, 24 November 1679.
  12. ↑ Page 433 in H W Turnbull (ed.), Correspondence of Isaac Newton, Vol 2 (1676–1687), (Cambridge University Press, 1960), document #286, 27 May 1686.
  13. 1 2 Pages 435–440 in H W Turnbull (ed.), Correspondence of Isaac Newton, Vol 2 (1676–1687), (Cambridge University Press, 1960), document #288, 20 June 1686.
  14. ↑ Page 436, Correspondence, Vol.2, already cited.
  15. ↑ Propositions 70 to 75 in Book 1, for example in the 1729 English translation of the Principia, start at page 263.
  16. ↑ Propositions 43 to 45 in Book 1, in the 1729 English translation of the Principia, start at page 177.
  17. ↑ See especially pp. 13–20 in Whiteside, D. T. (1991). "The Prehistory of the 'Principia' from 1664 to 1686". Notes and Records of the Royal Society of London. 45 (1): 11–61. doi: 10.1098/rsnr.1991.0002 . JSTOR   531520.
  18. ↑ See J. Bruce Brackenridge, "The key to Newton's dynamics: the Kepler problem and the Principia", (University of California Press, 1995), especially at pages 20–21.
  19. ↑ See for example the 1729 English translation of the Principia, at page 66.
  20. ↑ See especially p. 10 in Whiteside, D. T. (1970). "Before the Principia: The Maturing of Newton's Thoughts on Dynamical Astronomy, 1664–1684". Journal for the History of Astronomy. 1: 5–19. Bibcode:1970JHA.....1....5W. doi:10.1177/002182867000100103. S2CID   125845242.
  21. ↑ Gal, Ofer (2005). "The Invention of Celestial Mechanics". Early Science and Medicine. 10 (4): 529–534. doi:10.1163/157338205774661834. JSTOR   4130422.
  22. ↑ Guicciardini, Niccolò (2005). "Reconsidering the Hooke–Newton Debate on Gravitation: Recent Results". Early Science and Medicine. 10 (4): 510–517. doi:10.1163/157338205774661825. JSTOR   4130420.
  23. ↑ Nauenberg, M. (2005). "Hooke's and Newton's Contributions to the Early Development of Orbital mechanics and Universal Gravitation". Early Science and Medicine. 10 (4): 518–528. doi:10.1163/157338205774661861. JSTOR   4130421.
  24. ↑ See for example the results of Propositions 43–45 and 70–75 in Book 1, cited above.
  25. ↑ See also G E Smith, in Stanford Encyclopedia of Philosophy, "Newton's Philosophiae Naturalis Principia Mathematica".
  26. 1 2 Rowlands, Peter (2017). Newton And The Great World System. World Scientific Publishing. pp. 139–140, 146, 148–150. ISBN   9781786343758.
  27. ↑ The second extract is quoted and translated in W.W. Rouse Ball, "An Essay on Newton's 'Principia'" (London and New York: Macmillan, 1893), at page 69.
  28. ↑ The original statements by Clairaut (in French) are found (with orthography here as in the original) in "Explication abregée du systême du monde, et explication des principaux phénomenes astronomiques tirée des Principes de M. Newton" (1759), at Introduction (section IX), page 6: "Il ne faut pas croire que cette idée ... de Hook diminue la gloire de M. Newton", and "L'exemple de Hook" [serve] "à faire voir quelle distance il y a entre une vérité entrevue & une vérité démontrée".
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.