A mathematical model is an abstract description of a concrete system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in applied mathematics and in the natural sciences and engineering disciplines, as well as in non-physical systems such as the social sciences. It can also be taught as a subject in its own right.

In physics, mathematics, engineering, and related fields, a wave is a propagating dynamic disturbance of one or more quantities. Periodic waves oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a traveling wave; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a standing wave. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero. Waves are often described by a wave equation or a one-way wave equation for single wave propagation in a defined direction.

In mathematics and physics, a soliton is a nonlinear, self-reinforcing, localized wave packet that is strongly stable, in that it preserves its shape while propagating freely, at constant velocity, and recovers it even after collisions with other such localized wave packets. Its remarkable stability can be traced to a balanced cancellation of nonlinear and dispersive effects in the medium. Solitons were subsequently found to provide stable solutions of a wide class of weakly nonlinear dispersive partial differential equations describing physical systems.

In mathematics, a partial differential equation (PDE) is an equation which computes a function between various partial derivatives of a multivariable function.

The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after Erwin Schrödinger, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, source reconstruction in acoustics, or calculating the density of the Earth from measurements of its gravity field. It is called an inverse problem because it starts with the effects and then calculates the causes. It is the inverse of a forward problem, which starts with the causes and then calculates the effects.

The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So that if input A produces response X and input B produces response Y then input (A + B) produces response (X + Y).

In theoretical physics, the (one-dimensional) nonlinear Schrödinger equation (NLSE) is a nonlinear variation of the Schrödinger equation. It is a classical field equation whose principal applications are to the propagation of light in nonlinear optical fibers and planar waveguides and to Bose–Einstein condensates confined to highly anisotropic, cigar-shaped traps, in the mean-field regime. Additionally, the equation appears in the studies of small-amplitude gravity waves on the surface of deep inviscid (zero-viscosity) water; the Langmuir waves in hot plasmas; the propagation of plane-diffracted wave beams in the focusing regions of the ionosphere; the propagation of Davydov's alpha-helix solitons, which are responsible for energy transport along molecular chains; and many others. More generally, the NLSE appears as one of universal equations that describe the evolution of slowly varying packets of quasi-monochromatic waves in weakly nonlinear media that have dispersion. Unlike the linear Schrödinger equation, the NLSE never describes the time evolution of a quantum state. The 1D NLSE is an example of an integrable model.

In physics, a breather is a nonlinear wave in which energy concentrates in a localized and oscillatory fashion. This contradicts with the expectations derived from the corresponding linear system for infinitesimal amplitudes, which tends towards an even distribution of initially localized energy.
In mathematics, integrability is a property of certain dynamical systems. While there are several distinct formal definitions, informally speaking, an integrable system is a dynamical system with sufficiently many conserved quantities, or first integrals, that its motion is confined to a submanifold of much smaller dimensionality than that of its phase space.
Asım Orhan Barut was a Turkish-American theoretical physicist.
A parametric array, in the field of acoustics, is a nonlinear transduction mechanism that generates narrow, nearly side lobe-free beams of low frequency sound, through the mixing and interaction of high frequency sound waves, effectively overcoming the diffraction limit associated with linear acoustics. The main side lobe-free beam of low frequency sound is created as a result of nonlinear mixing of two high frequency sound beams at their difference frequency. Parametric arrays can be formed in water, air, and earth materials/rock.
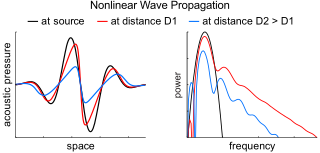
Nonlinear acoustics (NLA) is a branch of physics and acoustics dealing with sound waves of sufficiently large amplitudes. Large amplitudes require using full systems of governing equations of fluid dynamics and elasticity. These equations are generally nonlinear, and their traditional linearization is no longer possible. The solutions of these equations show that, due to the effects of nonlinearity, sound waves are being distorted as they travel.
In optics, the term soliton is used to refer to any optical field that does not change during propagation because of a delicate balance between nonlinear and dispersive effects in the medium. There are two main kinds of solitons:
In theoretical physics, the logarithmic Schrödinger equation is one of the nonlinear modifications of Schrödinger's equation. It is a classical wave equation with applications to extensions of quantum mechanics, quantum optics, nuclear physics, transport and diffusion phenomena, open quantum systems and information theory, effective quantum gravity and physical vacuum models and theory of superfluidity and Bose–Einstein condensation. Its relativistic version was first proposed by Gerald Rosen. It is an example of an integrable model.
The index of physics articles is split into multiple pages due to its size.
The index of physics articles is split into multiple pages due to its size.
Alexander G. Ramm is an American mathematician. His research focuses on differential and integral equations, operator theory, ill-posed and inverse problems, scattering theory, functional analysis, spectral theory, numerical analysis, theoretical electrical engineering, signal estimation, and tomography.
Walter Alexander Strauss is an American applied mathematician, specializing in partial differential equations and nonlinear waves. His research interests include partial differential equations, mathematical physics, stability theory, solitary waves, kinetic theory of plasmas, scattering theory, water waves, and dispersive waves.
In nonlinear systems, the three-wave equations, sometimes called the three-wave resonant interaction equations or triad resonances, describe small-amplitude waves in a variety of non-linear media, including electrical circuits and non-linear optics. They are a set of completely integrable nonlinear partial differential equations. Because they provide the simplest, most direct example of a resonant interaction, have broad applicability in the sciences, and are completely integrable, they have been intensively studied since the 1970s.







