In mathematics and physics, the notion of orientation entanglement is sometimes [1] used to develop intuition relating to the geometry of spinors or alternatively as a concrete realization of the failure of the special orthogonal groups to be simply connected.
Spatial vectors alone are not sufficient to describe fully the properties of rotations in space.
Consider the following example. [2] A coffee cup is suspended in a room by a pair of elastic rubber bands fixed to the walls of the room. The cup is rotated by its handle through a full twist of 360°, so that the handle is brought all the way around the central vertical axis of the cup and back to its original position.
Note that after this rotation, the cup has been returned to its original orientation, but that its orientation with respect to the walls is twisted. In other words, if we lower the coffee cup to the floor of the room, the two bands will coil around each other in one full twist of a double helix. This is an example of orientation entanglement: the new orientation of the coffee cup embedded in the room is not actually the same as the old orientation, as evidenced by the twisting of the rubber bands. Stated another way, the orientation of the coffee cup has become entangled with the orientation of the surrounding walls.
Clearly the geometry of spatial vectors alone is insufficient to express the orientation entanglement (the twist of the rubber bands). Consider drawing a vector across the cup. A full rotation will move the vector around so that the new orientation of the vector is the same as the old one. The vector alone doesn't know that the coffee cup is entangled with the walls of the room.
In fact, the coffee cup is inextricably entangled. There is no way to untwist the bands without rotating the cup. However, consider what happens instead when the cup is rotated, not through just one 360° turn, but two 360° turns for a total rotation of 720°. Then if the cup is lowered to the floor, the two rubber bands coil around each other in two full twists of a double helix. If the cup is now brought up through the center of one coil of this helix, and passed onto its other side, the twist disappears. The bands are no longer coiled about each other, even though no additional rotation had to be performed. (This experiment is more easily performed with a ribbon or belt. See below.)
Thus, whereas the orientation of the cup was twisted with respect to the walls after a rotation of only 360°, it was no longer twisted after a rotation of 720°. By only considering the vector attached to the cup, it is impossible to distinguish between these two cases, however. It is only when we attach a spinor to the cup that we can distinguish between the twisted and untwisted case.
In this situation, a spinor is a sort of polarized vector. In the adjacent diagram, a spinor can be represented as a vector whose head is a flag lying on one side of a Möbius strip, pointing inward. Initially, suppose that the flag is on top of the strip as shown. As the coffee cup is rotated it carries the spinor, and its flag, along the strip. If the cup is rotated through 360°, the spinor returns to the initial position, but the flag is now underneath the strip, pointing outward. It takes another 360° rotation in order to return the flag to its original orientation.
A detailed bridge between the above, and the formal mathematics can be found in the article on tangloids.
In three dimensions, the problem illustrated above corresponds to the fact that the Lie group SO(3) is not simply connected. Mathematically, one can tackle this problem by exhibiting the special unitary group, SU(2), which is also the spin group in three Euclidean dimensions, as a double cover of SO(3). If X = (x1, x2, x3) is a vector in R3, then we identify X with the 2 × 2 matrix with complex entries
Note that −det(X) gives the square of the Euclidean length of X regarded as a vector, and that X is a trace-free, or better, trace-zero Hermitian matrix.
The unitary group acts on X via
where M ∈ SU(2). Note that, since M is unitary,
Hence SU(2) acts via rotation on the vectors X. Conversely, since any change of basis which sends trace-zero Hermitian matrices to trace-zero Hermitian matrices must be unitary, it follows that every rotation also lifts to SU(2). However, each rotation is obtained from a pair of elements M and −M of SU(2). Hence SU(2) is a double-cover of SO(3). Furthermore, SU(2) is easily seen to be itself simply connected by realizing it as the group of unit quaternions, a space homeomorphic to the 3-sphere.
A unit quaternion has the cosine of half the rotation angle as its scalar part and the sine of half the rotation angle multiplying a unit vector along some rotation axis (here assumed fixed) as its pseudovector (or axial vector) part. If the initial orientation of a rigid body (with unentangled connections to its fixed surroundings) is identified with a unit quaternion having a zero pseudovector part and +1 for the scalar part, then after one complete rotation (2π rad) the pseudovector part returns to zero and the scalar part has become −1 (entangled). After two complete rotations (4π rad) the pseudovector part again returns to zero and the scalar part returns to +1 (unentangled), completing the cycle.
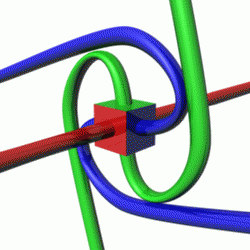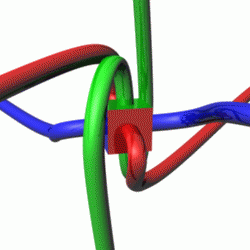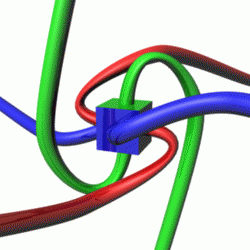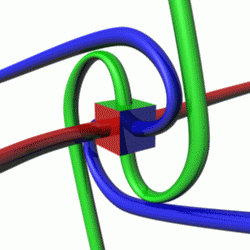
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. However, when a sequence of such small rotations is composed (integrated) to form an overall final rotation, the resulting spinor transformation depends on which sequence of small rotations was used. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360°. This property characterizes spinors: spinors can be viewed as the "square roots" of vectors.
In mathematics, physics and engineering, a Euclidean vector or simply a vector is a geometric object that has magnitude and direction. Vectors can be added to other vectors according to vector algebra. A Euclidean vector is frequently represented by a directed line segment, or graphically as an arrow connecting an initial pointA with a terminal pointB, and denoted by .
Vector calculus, or vector analysis, is concerned with differentiation and integration of vector fields, primarily in 3-dimensional Euclidean space The term "vector calculus" is sometimes used as a synonym for the broader subject of multivariable calculus, which spans vector calculus as well as partial differentiation and multiple integration. Vector calculus plays an important role in differential geometry and in the study of partial differential equations. It is used extensively in physics and engineering, especially in the description of electromagnetic fields, gravitational fields, and fluid flow.
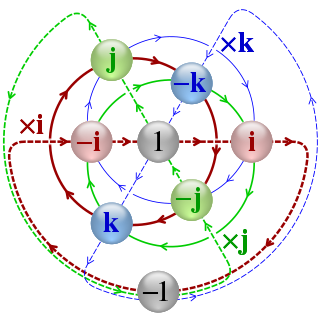
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space, or, equivalently, as the quotient of two vectors. Multiplication of quaternions is noncommutative.
Tangloids is a mathematical game for two players created by Piet Hein to model the calculus of spinors.
In physics, angular velocity or rotational velocity, also known as angular frequency vector, is a vector measure of rotation rate, that refers to how fast an object rotates or revolves relative to another point, i.e. how fast the angular position or orientation of an object changes with time.
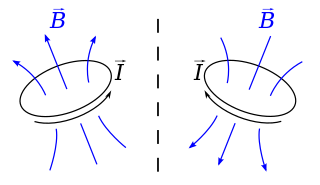
In physics and mathematics, a pseudovector is a quantity that is defined as a function of some vectors or other geometric shapes, that resembles a vector, and behaves like a vector in many situations, but is changed into its opposite if the orientation of the space is changed, or an improper rigid transformation such as a reflection is applied to the whole figure. Geometrically, the direction of a reflected pseudovector is opposite to its mirror image, but with equal magnitude. In contrast, the reflection of a true vector is exactly the same as its mirror image.
In mathematics, the special unitary group of degree n, denoted SU(n), is the Lie group of n × n unitary matrices with determinant 1.
Unit quaternions, known as versors, provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional space. Specifically, they encode information about an axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and crystallographic texture analysis.
Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have sign : a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space.
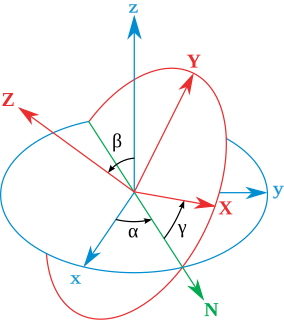
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body with respect to a fixed coordinate system.
In particle physics, a vector boson is a boson whose spin equals one. The vector bosons that are regarded as elementary particles in the Standard Model are the gauge bosons, the force carriers of fundamental interactions: the photon of electromagnetism, the W and Z bosons of the weak interaction, and the gluons of the strong interaction. Some composite particles are vector bosons, for instance any vector meson. During the 1970s and 1980s, intermediate vector bosons drew much attention in particle physics.
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix
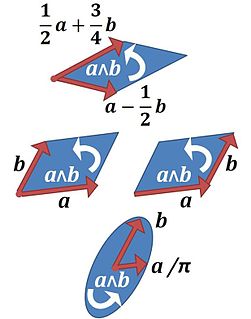
In mathematics, a bivector or 2-vector is a quantity in exterior algebra or geometric algebra that extends the idea of scalars and vectors. If a scalar is considered a degree zero quantity, and a vector is a degree one quantity, then a bivector can be thought of as being of degree two. Bivectors have applications in many areas of mathematics and physics. They are related to complex numbers in two dimensions and to both pseudovectors and quaternions in three dimensions. They can be used to generate rotations in any number of dimensions, and are a useful tool for classifying such rotations. They are also used in physics, tying together a number of otherwise unrelated quantities.
In mathematics, a versor is a quaternion of norm one. The word is derived from Latin versare = "to turn" with the suffix -or forming a noun from the verb. It was introduced by William Rowan Hamilton in the context of his quaternion theory.
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.
In mathematics, the spinor concept as specialised to three dimensions can be treated by means of the traditional notions of dot product and cross product. This is part of the detailed algebraic discussion of the rotation group SO(3).
In mathematics and physics, the plate trick, also known as Dirac's string trick, the belt trick, or the Balinese cup trick, is any of several demonstrations of the idea that rotating an object with strings attached to it by 360 degrees does not return the system to its original state, while a second rotation of 360 degrees, a total rotation of 720 degrees, does. Mathematically, it is a demonstration of the theorem that SU(2) is simply connected. To say that SU(2) double-covers SO(3) essentially means that the unit quaternions represent the group of rotations twice over. A detailed, intuitive, yet semi-formal articulation can be found in the article on tangloids.
In mathematics and mechanics, the Euler–Rodrigues formula describes the rotation of a vector in three dimensions. It is based on Rodrigues' rotation formula, but uses a different parametrization.
Symmetries in quantum mechanics describe features of spacetime and particles which are unchanged under some transformation, in the context of quantum mechanics, relativistic quantum mechanics and quantum field theory, and with applications in the mathematical formulation of the standard model and condensed matter physics. In general, symmetry in physics, invariance, and conservation laws, are fundamentally important constraints for formulating physical theories and models. In practice, they are powerful methods for solving problems and predicting what can happen. While conservation laws do not always give the answer to the problem directly, they form the correct constraints and the first steps to solving a multitude of problems.
