
The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
Density-functional theory (DFT) is a computational quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using functionals, i.e. functions of another function. In the case of DFT, these are functionals of the spatially dependent electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry.
In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a functional to a change in a function on which the functional depends.

In fluid dynamics, the Euler equations are a set of quasilinear partial differential equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. In particular, they correspond to the Navier–Stokes equations with zero viscosity and zero thermal conductivity.
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state.
Time-dependent density-functional theory (TDDFT) is a quantum mechanical theory used in physics and chemistry to investigate the properties and dynamics of many-body systems in the presence of time-dependent potentials, such as electric or magnetic fields. The effect of such fields on molecules and solids can be studied with TDDFT to extract features like excitation energies, frequency-dependent response properties, and photoabsorption spectra.

In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density is the quantity of charge per unit volume, measured in the SI system in coulombs per cubic meter (C⋅m−3), at any point in a volume. Surface charge density (σ) is the quantity of charge per unit area, measured in coulombs per square meter (C⋅m−2), at any point on a surface charge distribution on a two dimensional surface. Linear charge density (λ) is the quantity of charge per unit length, measured in coulombs per meter (C⋅m−1), at any point on a line charge distribution. Charge density can be either positive or negative, since electric charge can be either positive or negative.
Local-density approximations (LDA) are a class of approximations to the exchange–correlation (XC) energy functional in density functional theory (DFT) that depend solely upon the value of the electronic density at each point in space. Many approaches can yield local approximations to the XC energy. However, overwhelmingly successful local approximations are those that have been derived from the homogeneous electron gas (HEG) model. In this regard, LDA is generally synonymous with functionals based on the HEG approximation, which are then applied to realistic systems.
In quantum mechanics, the probability current is a mathematical quantity describing the flow of probability. Specifically, if one thinks of probability as a heterogeneous fluid, then the probability current is the rate of flow of this fluid. It is a real vector that changes with space and time. Probability currents are analogous to mass currents in hydrodynamics and electric currents in electromagnetism. As in those fields, the probability current is related to the probability density function via a continuity equation. The probability current is invariant under gauge transformation.
The Kohn-Sham equations are a set of mathematical equations used in quantum mechanics to simplify the complex problem of understanding how electrons behave in atoms and molecules. They introduce fictitious non-interacting electrons and use them to find the most stable arrangement of electrons, which helps scientists understand and predict the properties of matter at the atomic and molecular scale.
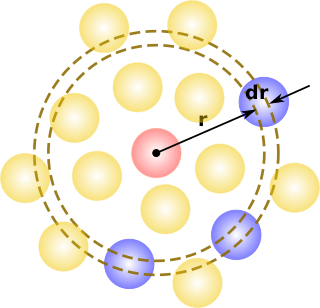
In statistical mechanics, the radial distribution function, in a system of particles, describes how density varies as a function of distance from a reference particle.
In atomic, molecular, and optical physics and quantum chemistry, the molecular Hamiltonian is the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule. This operator and the associated Schrödinger equation play a central role in computational chemistry and physics for computing properties of molecules and aggregates of molecules, such as thermal conductivity, specific heat, electrical conductivity, optical, and magnetic properties, and reactivity.
In statistical mechanics and thermodynamics the compressibility equation refers to an equation which relates the isothermal compressibility to the structure of the liquid. It reads:
In statistical mechanics the Percus–Yevick approximation is a closure relation to solve the Ornstein–Zernike equation. It is also referred to as the Percus–Yevick equation. It is commonly used in fluid theory to obtain e.g. expressions for the radial distribution function. The approximation is named after Jerome K. Percus and George J. Yevick.
In statistical mechanics the hypernetted-chain equation is a closure relation to solve the Ornstein–Zernike equation which relates the direct correlation function to the total correlation function. It is commonly used in fluid theory to obtain e.g. expressions for the radial distribution function. It is given by:
In quantum mechanics, specifically time-dependent density functional theory, the Runge–Gross theorem shows that for a many-body system evolving from a given initial wavefunction, there exists a one-to-one mapping between the potential in which the system evolves and the density of the system. The potentials under which the theorem holds are defined up to an additive purely time-dependent function: such functions only change the phase of the wavefunction and leave the density invariant. Most often the RG theorem is applied to molecular systems where the electronic density, ρ(r,t) changes in response to an external scalar potential, v(r,t), such as a time-varying electric field.
This is a glossary for the terminology often encountered in undergraduate quantum mechanics courses.
Quantum stochastic calculus is a generalization of stochastic calculus to noncommuting variables. The tools provided by quantum stochastic calculus are of great use for modeling the random evolution of systems undergoing measurement, as in quantum trajectories. Just as the Lindblad master equation provides a quantum generalization to the Fokker–Planck equation, quantum stochastic calculus allows for the derivation of quantum stochastic differential equations (QSDE) that are analogous to classical Langevin equations.
In computational chemistry, a solvent model is a computational method that accounts for the behavior of solvated condensed phases. Solvent models enable simulations and thermodynamic calculations applicable to reactions and processes which take place in solution. These include biological, chemical and environmental processes. Such calculations can lead to new predictions about the physical processes occurring by improved understanding.
The linearized augmented-plane-wave method (LAPW) is an implementation of Kohn-Sham density functional theory (DFT) adapted to periodic materials. It typically goes along with the treatment of both valence and core electrons on the same footing in the context of DFT and the treatment of the full potential and charge density without any shape approximation. This is often referred to as the all-electron full-potential linearized augmented-plane-wave method (FLAPW). It does not rely on the pseudopotential approximation and employs a systematically extendable basis set. These features make it one of the most precise implementations of DFT, applicable to all crystalline materials, regardless of their chemical composition. It can be used as a reference for evaluating other approaches.






















