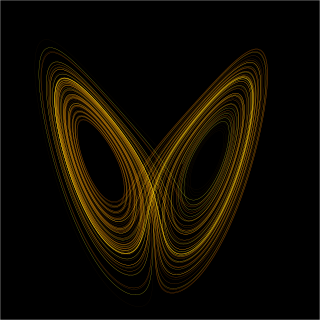
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a lake.

In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.

In mathematics, the Wronskian is a determinant introduced by Józef Hoene-Wroński (1812) and named by Thomas Muir. It is used in the study of differential equations, where it can sometimes show linear independence in a set of solutions.

In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation.

In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions.
In mathematics, integral equations are equations in which an unknown function appears under an integral sign.
In mathematics and its applications, classical Sturm–Liouville theory is the theory of real second-order linear ordinary differential equations of the form:

In mathematics, a differential equation is an equation that relates one or more functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common; therefore, differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology.
In mathematics, and in particular in the theory of solitons, the Dym equation (HD) is the third-order partial differential equation
Floquet theory is a branch of the theory of ordinary differential equations relating to the class of solutions to periodic linear differential equations of the form

In mathematics, specifically in the study of ordinary differential equations, the Peano existence theorem, Peano theorem or Cauchy–Peano theorem, named after Giuseppe Peano and Augustin-Louis Cauchy, is a fundamental theorem which guarantees the existence of solutions to certain initial value problems.
In mathematics, in the field of ordinary differential equations, the Kneser theorem, named after Adolf Kneser, provides criteria to decide whether a differential equation is oscillating or not.
In mathematics, in the field of ordinary differential equations, the Sturm–Picone comparison theorem, named after Jacques Charles François Sturm and Mauro Picone, is a classical theorem which provides criteria for the oscillation and non-oscillation of solutions of certain linear differential equations in the real domain.

In mathematics, in the field of ordinary differential equations, Sturm separation theorem, named after Jacques Charles François Sturm, describes the location of roots of solutions of homogeneous second order linear differential equations. Basically the theorem states that given two linear independent solutions of such an equation the zeros of the two solutions are alternating.
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation. In his dissertation Hermann Weyl generalized the classical Sturm–Liouville theory on a finite closed interval to second order differential operators with singularities at the endpoints of the interval, possibly semi-infinite or infinite. Unlike the classical case, the spectrum may no longer consist of just a countable set of eigenvalues, but may also contain a continuous part. In this case the eigenfunction expansion involves an integral over the continuous part with respect to a spectral measure, given by the Titchmarsh–Kodaira formula. The theory was put in its final simplified form for singular differential equations of even degree by Kodaira and others, using von Neumann's spectral theorem. It has had important applications in quantum mechanics, operator theory and harmonic analysis on semisimple Lie groups.

Gerald Teschl is an Austrian mathematical physicist and professor of mathematics. He works in the area of mathematical physics; in particular direct and inverse spectral theory with application to completely integrable partial differential equations.

In mathematics, an ordinary differential equation (ODE) is a differential equation containing one or more functions of one independent variable and the derivatives of those functions. The term ordinary is used in contrast with the term partial differential equation which may be with respect to more than one independent variable.
In applied mathematics, the Atkinson–Mingarelli theorem, named after Frederick Valentine Atkinson and A. B. Mingarelli, concerns eigenvalues of certain Sturm–Liouville differential operators.
In mathematics a Cauchy–Euler operator is a differential operator of the form for a polynomial p. It is named after Augustin-Louis Cauchy and Leonhard Euler. The simplest example is that in which p(x) = x, which has eigenvalues n = 0, 1, 2, 3, ... and corresponding eigenfunctions xn.







