
Mathematical physics refers to the development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines the field as "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and for the formulation of physical theories". An alternative definition would also include those mathematics that are inspired by physics.

Carl Gustav Jacob Jacobi was a German mathematician who made fundamental contributions to elliptic functions, dynamics, differential equations, determinants, and number theory. His name is occasionally written as Carolus Gustavus Iacobus Iacobi in his Latin books, and his first name is sometimes given as Karl.
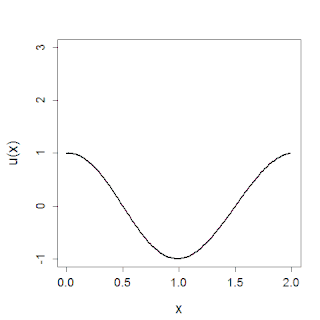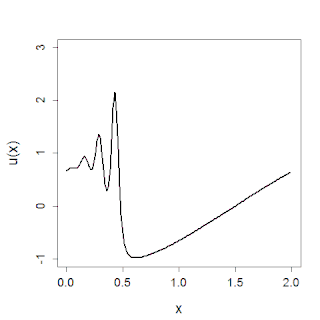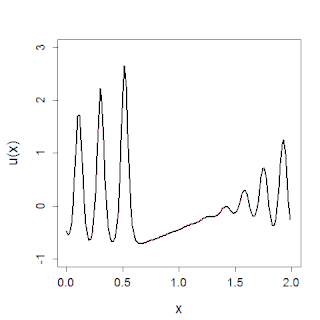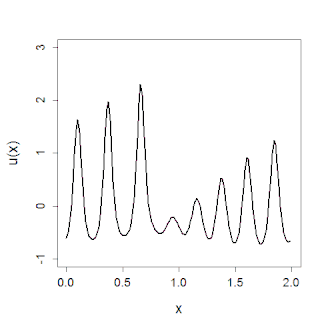
In mathematics, the Korteweg–De Vries (KdV) equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified. KdV can be solved by means of the inverse scattering transform. The mathematical theory behind the KdV equation is a topic of active research. The KdV equation was first introduced by Boussinesq and rediscovered by Diederik Korteweg and Gustav de Vries (1895).
In mathematics and physics, the inverse scattering problem is the problem of determining characteristics of an object, based on data of how it scatters incoming radiation or particles. It is the inverse problem to the direct scattering problem, which is to determine how radiation or particles are scattered based on the properties of the scatterer.

Sergei Petrovich Novikov is a Soviet and Russian mathematician, noted for work in both algebraic topology and soliton theory. In 1970, he won the Fields Medal.
In mathematics, and in particular in the theory of solitons, the Dym equation (HD) is the third-order partial differential equation
In mathematics, integrability is a property of certain dynamical systems. While there are several distinct formal definitions, informally speaking, an integrable system is a dynamical system with sufficiently many conserved quantities, or first integrals, such that its behaviour has far fewer degrees of freedom than the dimensionality of its phase space; that is, its evolution is restricted to a submanifold within its phase space.
In mathematics, the composition operator with symbol is a linear operator defined by the rule
In mathematics, the Poincaré–Bendixson theorem is a statement about the long-term behaviour of orbits of continuous dynamical systems on the plane, cylinder, or two-sphere.
The Toda lattice, introduced by Morikazu Toda (1967), is a simple model for a one-dimensional crystal in solid state physics. It is famous because it is one of the earliest examples of a non-linear completely integrable system.

In the mathematical study of heat conduction and diffusion, a heat kernel is the fundamental solution to the heat equation on a specified domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectrum of the Laplace operator, and is thus of some auxiliary importance throughout mathematical physics. The heat kernel represents the evolution of temperature in a region whose boundary is held fixed at a particular temperature, such that an initial unit of heat energy is placed at a point at time t = 0.
Graduate Studies in Mathematics (GSM) is a series of graduate-level textbooks in mathematics published by the American Mathematical Society (AMS). The books in this series are published in hardcover and e-book formats.
In mathematics, the Kneser theorem can refer to two distinct theorems in the field of ordinary differential equations:
In mathematics, in the field of ordinary differential equations, a nontrivial solution to an ordinary differential equation
Michio Jimbo is a Japanese mathematician working in mathematical physics and is a professor of mathematics at Rikkyo University. He is a grandson of the linguist Kaku Jimbo.

Friedrich "Fritz" Gesztesy is a well-known Austrian-American mathematical physicist and Professor of Mathematics at Baylor University, known for his important contributions in spectral theory, functional analysis, nonrelativistic quantum mechanics, ordinary and partial differential operators, and completely integrable systems. He has authored more than 270 publications on mathematics and physics.
A Jacobi operator, also known as Jacobi matrix, is a symmetric linear operator acting on sequences which is given by an infinite tridiagonal matrix. It is commonly used to specify systems of orthonormal polynomials over a finite, positive Borel measure. This operator is named after Carl Gustav Jacob Jacobi.

Sergio Albeverio is a Swiss mathematician and mathematical physicist working in numerous fields of mathematics and its applications. In particular he is known for his work in probability theory, analysis, mathematical physics, and in the areas algebra, geometry, number theory, as well as in applications, from natural to social-economic sciences.
Michael Eugene Taylor is an American mathematician, working in partial differential equations.

Tetsuji Miwa is a Japanese mathematician, specializing in mathematical physics.
This page is based on this
Wikipedia article Text is available under the
CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.








