In mathematics, specifically category theory, an overcategory (also called a slice category), as well as an undercategory (also called a coslice category), is a distinguished class of categories used in multiple contexts, such as with covering spaces (espace etale). They were introduced as a mechanism for keeping track of data surrounding a fixed object in some category . There is a dual notion of undercategory, which is defined similarly.
Let be a category and a fixed object of [1] pg 59. The overcategory (also called a slice category) is an associated category whose objects are pairs where is a morphism in . Then, a morphism between objects is given by a morphism in the category such that the following diagram commutes
There is a dual notion called the undercategory (also called a coslice category) whose objects are pairs where is a morphism in . Then, morphisms in are given by morphisms in such that the following diagram commutes
These two notions have generalizations in 2-category theory [2] and higher category theory [3] pg 43, with definitions either analogous or essentially the same.
Many categorical properties of are inherited by the associated over and undercategories for an object . For example, if has finite products and coproducts, it is immediate the categories and have these properties since the product and coproduct can be constructed in , and through universal properties, there exists a unique morphism either to or from . In addition, this applies to limits and colimits as well.
Recall that a site is a categorical generalization of a topological space first introduced by Grothendieck. One of the canonical examples comes directly from topology, where the category whose objects are open subsets of some topological space , and the morphisms are given by inclusion maps. Then, for a fixed open subset , the overcategory is canonically equivalent to the category for the induced topology on . This is because every object in is an open subset contained in .
The category of commutative -algebras is equivalent to the undercategory for the category of commutative rings. This is because the structure of an -algebra on a commutative ring is directly encoded by a ring morphism . If we consider the opposite category, it is an overcategory of affine schemes, , or just .
Another common overcategory considered in the literature are overcategories of spaces, such as schemes, smooth manifolds, or topological spaces. These categories encode objects relative to a fixed object, such as the category of schemes over , . Fiber products in these categories can be considered intersections, given the objects are subobjects of the fixed object.
In mathematics, one can often define a direct product of objects already known, giving a new one. This induces a structure on the Cartesian product of the underlying sets from that of the contributing objects. More abstractly, one talks about the product in category theory, which formalizes these notions.
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:
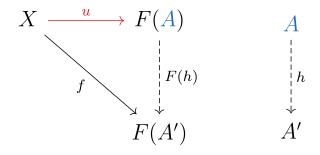
In mathematics, more specifically in category theory, a universal property is a property that characterizes up to an isomorphism the result of some constructions. Thus, universal properties can be used for defining some objects independently from the method chosen for constructing them. For example, the definitions of the integers from the natural numbers, of the rational numbers from the integers, of the real numbers from the rational numbers, and of polynomial rings from the field of their coefficients can all be done in terms of universal properties. In particular, the concept of universal property allows a simple proof that all constructions of real numbers are equivalent: it suffices to prove that they satisfy the same universal property.
In commutative algebra, the prime spectrum of a commutative ring R is the set of all prime ideals of R, and is usually denoted by ; in algebraic geometry it is simultaneously a topological space equipped with the sheaf of rings .
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits.
In mathematics, specifically category theory, adjunction is a relationship that two functors may exhibit, intuitively corresponding to a weak form of equivalence between two related categories. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
In mathematics, specifically in category theory, a pre-abelian category is an additive category that has all kernels and cokernels.
In category theory, a category is Cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in that their internal language is the simply typed lambda calculus. They are generalized by closed monoidal categories, whose internal language, linear type systems, are suitable for both quantum and classical computation.
In mathematics, a sheaf is a tool for systematically tracking data attached to the open sets of a topological space and defined locally with regard to them. For example, for each open set, the data could be the ring of continuous functions defined on that open set. Such data are well behaved in that they can be restricted to smaller open sets, and also the data assigned to an open set are equivalent to all collections of compatible data assigned to collections of smaller open sets covering the original open set.
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain. The pushout consists of an object P along with two morphisms X → P and Y → P that complete a commutative square with the two given morphisms f and g. In fact, the defining universal property of the pushout essentially says that the pushout is the "most general" way to complete this commutative square. Common notations for the pushout are and .
In mathematics, a gerbe is a construct in homological algebra and topology. Gerbes were introduced by Jean Giraud following ideas of Alexandre Grothendieck as a tool for non-commutative cohomology in degree 2. They can be seen as an analogue of fibre bundles where the fibre is the classifying stack of a group. Gerbes provide a convenient, if highly abstract, language for dealing with many types of deformation questions especially in modern algebraic geometry. In addition, special cases of gerbes have been used more recently in differential topology and differential geometry to give alternative descriptions to certain cohomology classes and additional structures attached to them.
In mathematics, a comma category is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W. Lawvere, although the technique did not become generally known until many years later. Several mathematical concepts can be treated as comma categories. Comma categories also guarantee the existence of some limits and colimits. The name comes from the notation originally used by Lawvere, which involved the comma punctuation mark. The name persists even though standard notation has changed, since the use of a comma as an operator is potentially confusing, and even Lawvere dislikes the uninformative term "comma category".
In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain. The pullback is written
In mathematics, Tannaka–Krein duality theory concerns the interaction of a compact topological group and its category of linear representations. It is a natural extension of Pontryagin duality, between compact and discrete commutative topological groups, to groups that are compact but noncommutative. The theory is named after Tadao Tannaka and Mark Grigorievich Krein. In contrast to the case of commutative groups considered by Lev Pontryagin, the notion dual to a noncommutative compact group is not a group, but a category of representations Π(G) with some additional structure, formed by the finite-dimensional representations of G.
In mathematics, the cotangent complex is a common generalisation of the cotangent sheaf, normal bundle and virtual tangent bundle of a map of geometric spaces such as manifolds or schemes. If is a morphism of geometric or algebraic objects, the corresponding cotangent complex can be thought of as a universal "linearization" of it, which serves to control the deformation theory of . It is constructed as an object in a certain derived category of sheaves on using the methods of homotopical algebra.
In mathematics, especially homotopy theory, the homotopy fiber is part of a construction that associates a fibration to an arbitrary continuous function of topological spaces . It acts as a homotopy theoretic kernel of a mapping of topological spaces due to the fact it yields a long exact sequence of homotopy groups
In mathematics, in the theory of Hopf algebras, a Hopf algebroid is a generalisation of weak Hopf algebras, certain skew Hopf algebras and commutative Hopf k-algebroids. If k is a field, a commutative k-algebroid is a cogroupoid object in the category of k-algebras; the category of such is hence dual to the category of groupoid k-schemes. This commutative version has been used in 1970-s in algebraic geometry and stable homotopy theory. The generalization of Hopf algebroids and its main part of the structure, associative bialgebroids, to the noncommutative base algebra was introduced by J.-H. Lu in 1996 as a result on work on groupoids in Poisson geometry. They may be loosely thought of as Hopf algebras over a noncommutative base ring, where weak Hopf algebras become Hopf algebras over a separable algebra. It is a theorem that a Hopf algebroid satisfying a finite projectivity condition over a separable algebra is a weak Hopf algebra, and conversely a weak Hopf algebra H is a Hopf algebroid over its separable subalgebra HL. The antipode axioms have been changed by G. Böhm and K. Szlachányi in 2004 for tensor categorical reasons and to accommodate examples associated to depth two Frobenius algebra extensions.
In algebraic geometry, a derived scheme is a homotopy-theoretic generalization of a scheme in which classical commutative rings are replaced with derived versions such as differential graded algebras, commutative simplicial rings, or commutative ring spectra.
In category theory, a branch of mathematics, an ∞-groupoid is an abstract homotopical model for topological spaces. One model uses Kan complexes which are fibrant objects in the category of simplicial sets. It is an ∞-category generalization of a groupoid, a category in which every morphism is an isomorphism.
