The subset sum problem (SSP) is a decision problem in computer science. In its most general formulation, there is a multiset of integers and a target-sum , and the question is to decide whether any subset of the integers sum to precisely . The problem is known to be NP-complete. Moreover, some restricted variants of it are NP-complete too, for example:
The bin packing problem is an optimization problem, in which items of different sizes must be packed into a finite number of bins or containers, each of a fixed given capacity, in a way that minimizes the number of bins used. The problem has many applications, such as filling up containers, loading trucks with weight capacity constraints, creating file backups in media, splitting a network prefix into multiple subnets, and technology mapping in FPGA semiconductor chip design.

In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor.

Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead.
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems with provable guarantees on the distance of the returned solution to the optimal one. Approximation algorithms naturally arise in the field of theoretical computer science as a consequence of the widely believed P ≠ NP conjecture. Under this conjecture, a wide class of optimization problems cannot be solved exactly in polynomial time. The field of approximation algorithms, therefore, tries to understand how closely it is possible to approximate optimal solutions to such problems in polynomial time. In an overwhelming majority of the cases, the guarantee of such algorithms is a multiplicative one expressed as an approximation ratio or approximation factor i.e., the optimal solution is always guaranteed to be within a (predetermined) multiplicative factor of the returned solution. However, there are also many approximation algorithms that provide an additive guarantee on the quality of the returned solution. A notable example of an approximation algorithm that provides both is the classic approximation algorithm of Lenstra, Shmoys and Tardos for scheduling on unrelated parallel machines.
In computer science, a polynomial-time approximation scheme (PTAS) is a type of approximation algorithm for optimization problems.
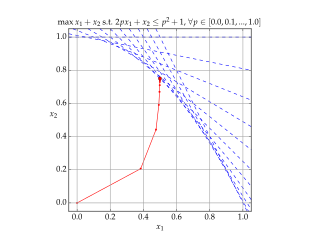
Interior-point methods are algorithms for solving linear and non-linear convex optimization problems. IPMs combine two advantages of previously-known algorithms:

In graph theory, a dominating set for a graph G is a subset D of its vertices, such that any vertex of G is in D, or has a neighbor in D. The domination numberγ(G) is the number of vertices in a smallest dominating set for G.
In computational complexity theory, the class APX is the set of NP optimization problems that allow polynomial-time approximation algorithms with approximation ratio bounded by a constant. In simple terms, problems in this class have efficient algorithms that can find an answer within some fixed multiplicative factor of the optimal answer.
A fully polynomial-time approximation scheme (FPTAS) is an algorithm for finding approximate solutions to function problems, especially optimization problems. An FPTAS takes as input an instance of the problem and a parameter ε > 0. It returns as output a value which is at least times the correct value, and at most times the correct value.
MAX-3SAT is a problem in the computational complexity subfield of computer science. It generalises the Boolean satisfiability problem (SAT) which is a decision problem considered in complexity theory. It is defined as:
In computer science, particularly the study of approximation algorithms, an L-reduction is a transformation of optimization problems which linearly preserves approximability features; it is one type of approximation-preserving reduction. L-reductions in studies of approximability of optimization problems play a similar role to that of polynomial reductions in the studies of computational complexity of decision problems.
In mathematical optimization, the ellipsoid method is an iterative method for minimizing convex functions over convex sets. The ellipsoid method generates a sequence of ellipsoids whose volume uniformly decreases at every step, thus enclosing a minimizer of a convex function.
In graph theory, the metric k-center problem or vertex k-center problem is a classical combinatorial optimization problem studied in theoretical computer science that is NP-hard. Given n cities with specified distances, one wants to build k warehouses in different cities and minimize the maximum distance of a city to a warehouse. In graph theory, this means finding a set of k vertices for which the largest distance of any point to its closest vertex in the k-set is minimum. The vertices must be in a metric space, providing a complete graph that satisfies the triangle inequality. It has application in facility location and clustering.
In computational complexity theory, a branch of computer science, the Max/min CSP/Ones classification theorems state necessary and sufficient conditions that determine the complexity classes of problems about satisfying a subset S of boolean relations. They are similar to Schaefer's dichotomy theorem, which classifies the complexity of satisfying finite sets of relations; however, the Max/min CSP/Ones classification theorems give information about the complexity of approximating an optimal solution to a problem defined by S.
In computational complexity theory, a gap reduction is a reduction to a particular type of decision problem, known as a c-gap problem. Such reductions provide information about the hardness of approximating solutions to optimization problems. In short, a gap problem refers to one wherein the objective is to distinguish between cases where the best solution is above one threshold from cases where the best solution is below another threshold, such that the two thresholds have a gap in between. Gap reductions can be used to demonstrate inapproximability results, as if a problem may be approximated to a better factor than the size of gap, then the approximation algorithm can be used to solve the corresponding gap problem.
In computability theory and computational complexity theory, especially the study of approximation algorithms, an approximation-preserving reduction is an algorithm for transforming one optimization problem into another problem, such that the distance of solutions from optimal is preserved to some degree. Approximation-preserving reductions are a subset of more general reductions in complexity theory; the difference is that approximation-preserving reductions usually make statements on approximation problems or optimization problems, as opposed to decision problems.
The Karmarkar–Karp (KK) bin packing algorithms are several related approximation algorithm for the bin packing problem. The bin packing problem is a problem of packing items of different sizes into bins of identical capacity, such that the total number of bins is as small as possible. Finding the optimal solution is computationally hard. Karmarkar and Karp devised an algorithm that runs in polynomial time and finds a solution with at most bins, where OPT is the number of bins in the optimal solution. They also devised several other algorithms with slightly different approximation guarantees and run-time bounds.
(Stochastic) variance reduction is an algorithmic approach to minimizing functions that can be decomposed into finite sums. By exploiting the finite sum structure, variance reduction techniques are able to achieve convergence rates that are impossible to achieve with methods that treat the objective as an infinite sum, as in the classical Stochastic approximation setting.
A parameterized approximation algorithm is a type of algorithm that aims to find approximate solutions to NP-hard optimization problems in polynomial time in the input size and a function of a specific parameter. These algorithms are designed to combine the best aspects of both traditional approximation algorithms and fixed-parameter tractability.










