In complex analysis, a partial fraction expansion is a way of writing a meromorphic function as an infinite sum of rational functions and polynomials. When is a rational function, this reduces to the usual method of partial fractions.
In complex analysis, a partial fraction expansion is a way of writing a meromorphic function as an infinite sum of rational functions and polynomials. When is a rational function, this reduces to the usual method of partial fractions.
By using polynomial long division and the partial fraction technique from algebra, any rational function can be written as a sum of terms of the form , where and are complex, is an integer, and is a polynomial. Just as polynomial factorization can be generalized to the Weierstrass factorization theorem, there is an analogy to partial fraction expansions for certain meromorphic functions.
A proper rational function (one for which the degree of the denominator is greater than the degree of the numerator) has a partial fraction expansion with no polynomial terms. Similarly, a meromorphic function for which goes to 0 as goes to infinity at least as quickly as has an expansion with no polynomial terms.
Let be a function meromorphic in the finite complex plane with poles at and let be a sequence of simple closed curves such that:
Suppose also that there exists an integer such that
Writing for the principal part of the Laurent expansion of about the point , we have
if . If , then
where the coefficients are given by
should be set to 0, because even if itself does not have a pole at 0, the residues of at must still be included in the sum.
Note that in the case of , we can use the Laurent expansion of about the origin to get
so that the polynomial terms contributed are exactly the regular part of the Laurent series up to .
For the other poles where , can be pulled out of the residue calculations:
The simplest meromorphic functions with an infinite number of poles are the non-entire trigonometric functions. As an example, is meromorphic with poles at , The contours will be squares with vertices at traversed counterclockwise, , which are easily seen to satisfy the necessary conditions.
On the horizontal sides of ,
so
for all real , which yields
For , is continuous, decreasing, and bounded below by 1, so it follows that on the horizontal sides of , . Similarly, it can be shown that on the vertical sides of .
With this bound on we can see that
That is, the maximum of on occurs at the minimum of , which is .
Therefore , and the partial fraction expansion of looks like
The principal parts and residues are easy enough to calculate, as all the poles of are simple and have residue -1:
We can ignore , since both and are analytic at 0, so there is no contribution to the sum, and ordering the poles so that , etc., gives
Because the partial fraction expansion often yields sums of , it can be useful in finding a way to write a function as an infinite product; integrating both sides gives a sum of logarithms, and exponentiating gives the desired product:
Applying some logarithm rules,
which finally gives
The partial fraction expansion for a function can also be used to find a Laurent series for it by simply replacing the rational functions in the sum with their Laurent series, which are often not difficult to write in closed form. This can also lead to interesting identities if a Laurent series is already known.
Recall that
We can expand the summand using a geometric series:
Substituting back,
which shows that the coefficients in the Laurent (Taylor) series of about are
where are the tangent numbers.
Conversely, we can compare this formula to the Taylor expansion for about to calculate the infinite sums:

Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions y(x) of Bessel's differential equation

In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points (cos t, sin t) form a circle with a unit radius, the points (cosh t, sinh t) form the right half of the unit hyperbola. Also, similarly to how the derivatives of sin(t) and cos(t) are cos(t) and –sin(t) respectively, the derivatives of sinh(t) and cosh(t) are cosh(t) and +sinh(t) respectively.
Integration is the basic operation in integral calculus. While differentiation has straightforward rules by which the derivative of a complicated function can be found by differentiating its simpler component functions, integration does not, so tables of known integrals are often useful. This page lists some of the most common antiderivatives.

In mathematics, the Gudermannian function relates a hyperbolic angle measure to a circular angle measure called the gudermannian of and denoted . The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude when parameter

In mathematics, the Clausen function, introduced by Thomas Clausen (1832), is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other forms. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function.
In mathematics, the Lerch zeta function, sometimes called the Hurwitz–Lerch zeta function, is a special function that generalizes the Hurwitz zeta function and the polylogarithm. It is named after Czech mathematician Mathias Lerch, who published a paper about the function in 1887.
In mathematics, a logarithm of a matrix is another matrix such that the matrix exponential of the latter matrix equals the original matrix. It is thus a generalization of the scalar logarithm and in some sense an inverse function of the matrix exponential. Not all matrices have a logarithm and those matrices that do have a logarithm may have more than one logarithm. The study of logarithms of matrices leads to Lie theory since when a matrix has a logarithm then it is in an element of a Lie group and the logarithm is the corresponding element of the vector space of the Lie algebra.

In mathematics, the lemniscate elliptic functions are elliptic functions related to the arc length of the lemniscate of Bernoulli. They were first studied by Giulio Fagnano in 1718 and later by Leonhard Euler and Carl Friedrich Gauss, among others.

In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opposite that angle to the length of the longest side of the triangle, and the cosine is the ratio of the length of the adjacent leg to that of the hypotenuse. For an angle , the sine and cosine functions are denoted simply as and .
In statistical mechanics, the two-dimensional square lattice Ising model is a simple lattice model of interacting magnetic spins. The model is notable for having nontrivial interactions, yet having an analytical solution. The model was solved by Lars Onsager for the special case that the external magnetic field H = 0. An analytical solution for the general case for has yet to be found.
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.
In mathematics, the Plancherel theorem for spherical functions is an important result in the representation theory of semisimple Lie groups, due in its final form to Harish-Chandra. It is a natural generalisation in non-commutative harmonic analysis of the Plancherel formula and Fourier inversion formula in the representation theory of the group of real numbers in classical harmonic analysis and has a similarly close interconnection with the theory of differential equations. It is the special case for zonal spherical functions of the general Plancherel theorem for semisimple Lie groups, also proved by Harish-Chandra. The Plancherel theorem gives the eigenfunction expansion of radial functions for the Laplacian operator on the associated symmetric space X; it also gives the direct integral decomposition into irreducible representations of the regular representation on L2(X). In the case of hyperbolic space, these expansions were known from prior results of Mehler, Weyl and Fock.
In discrete calculus the indefinite sum operator, denoted by or , is the linear operator, inverse of the forward difference operator . It relates to the forward difference operator as the indefinite integral relates to the derivative. Thus

In probability theory and directional statistics, a wrapped Cauchy distribution is a wrapped probability distribution that results from the "wrapping" of the Cauchy distribution around the unit circle. The Cauchy distribution is sometimes known as a Lorentzian distribution, and the wrapped Cauchy distribution may sometimes be referred to as a wrapped Lorentzian distribution.

In probability theory and directional statistics, a wrapped exponential distribution is a wrapped probability distribution that results from the "wrapping" of the exponential distribution around the unit circle.
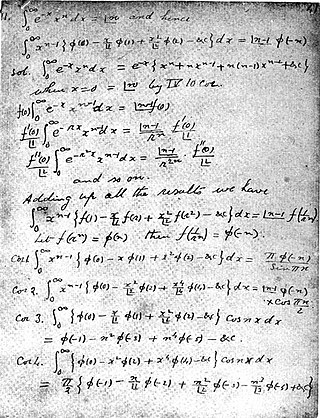
In mathematics, Ramanujan's Master Theorem, named after Srinivasa Ramanujan, is a technique that provides an analytic expression for the Mellin transform of an analytic function.