In mathematical analysis and in probability theory, a σ-algebra on a set X is a nonempty collection Σ of subsets of X closed under complement, countable unions, and countable intersections. The ordered pair is called a measurable space.
In combinatorics, a branch of mathematics, a matroid is a structure that abstracts and generalizes the notion of linear independence in vector spaces. There are many equivalent ways to define a matroid axiomatically, the most significant being in terms of: independent sets; bases or circuits; rank functions; closure operators; and closed sets or flats. In the language of partially ordered sets, a finite simple matroid is equivalent to a geometric lattice.
In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is sometimes called a planar matroid ; these are exactly the graphic matroids formed from planar graphs.

In geometry and combinatorics, an arrangement of hyperplanes is an arrangement of a finite set A of hyperplanes in a linear, affine, or projective space S. Questions about a hyperplane arrangement A generally concern geometrical, topological, or other properties of the complement, M(A), which is the set that remains when the hyperplanes are removed from the whole space. One may ask how these properties are related to the arrangement and its intersection semilattice. The intersection semilattice of A, written L(A), is the set of all subspaces that are obtained by intersecting some of the hyperplanes; among these subspaces are S itself, all the individual hyperplanes, all intersections of pairs of hyperplanes, etc. (excluding, in the affine case, the empty set). These intersection subspaces of A are also called the flats ofA. The intersection semilattice L(A) is partially ordered by reverse inclusion.
Pregeometry, and in full combinatorial pregeometry, are essentially synonyms for "matroid". They were introduced by Gian-Carlo Rota with the intention of providing a less "ineffably cacophonous" alternative term. Also, the term combinatorial geometry, sometimes abbreviated to geometry, was intended to replace "simple matroid". These terms are now infrequently used in the study of matroids.
In mathematics, a regular matroid is a matroid that can be represented over all fields.
In matroid theory, the dual of a matroid is another matroid that has the same elements as , and in which a set is independent if and only if has a basis set disjoint from it.
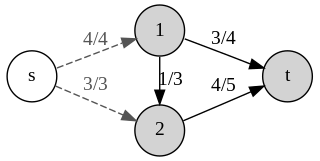
An oriented matroid is a mathematical structure that abstracts the properties of directed graphs, vector arrangements over ordered fields, and hyperplane arrangements over ordered fields. In comparison, an ordinary matroid abstracts the dependence properties that are common both to graphs, which are not necessarily directed, and to arrangements of vectors over fields, which are not necessarily ordered.
In mathematics, a uniform matroid is a matroid in which the independent sets are exactly the sets containing at most r elements, for some fixed integer r. An alternative definition is that every permutation of the elements is a symmetry.
In the mathematical theory of matroids, a minor of a matroid M is another matroid N that is obtained from M by a sequence of restriction and contraction operations. Matroid minors are closely related to graph minors, and the restriction and contraction operations by which they are formed correspond to edge deletion and edge contraction operations in graphs. The theory of matroid minors leads to structural decompositions of matroids, and characterizations of matroid families by forbidden minors, analogous to the corresponding theory in graphs.
Rota's excluded minors conjecture is one of a number of conjectures made by mathematician Gian-Carlo Rota. It is considered to be an important problem by some members of the structural combinatorics community. Rota conjectured in 1971 that, for every finite field, the family of matroids that can be represented over that field has only finitely many excluded minors. A proof of the conjecture has been announced by Geelen, Gerards, and Whittle.
In mathematics, a partition matroid or partitional matroid is a matroid that is a direct sum of uniform matroids. It is defined over a base set in which the elements are partitioned into different categories. For each category, there is a capacity constraint - a maximum number of allowed elements from this category. The independent sets of a partition matroid are exactly the sets in which, for each category, the number of elements from this category is at most the category capacity.
In matroid theory, an Eulerian matroid is a matroid whose elements can be partitioned into a collection of disjoint circuits.
In mathematics and computer science, a matroid oracle is a subroutine through which an algorithm may access a matroid, an abstract combinatorial structure that can be used to describe the linear dependencies between vectors in a vector space or the spanning trees of a graph, among other applications.
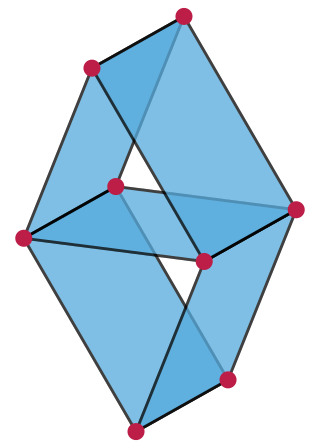
In mathematics, the Vámos matroid or Vámos cube is a matroid over a set of eight elements that cannot be represented as a matrix over any field. It is named after English mathematician Peter Vámos, who first described it in an unpublished manuscript in 1968.
In the mathematical theory of matroids, the rank of a matroid is the maximum size of an independent set in the matroid. The rank of a subset S of elements of the matroid is, similarly, the maximum size of an independent subset of S, and the rank function of the matroid maps sets of elements to their ranks.
In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.
In linear algebra and matroid theory, Rota's basis conjecture is an unproven conjecture concerning rearrangements of bases, named after Gian-Carlo Rota. It states that, if X is either a vector space of dimension n or more generally a matroid of rank n, with n disjoint bases Bi, then it is possible to arrange the elements of these bases into an n × n matrix in such a way that the rows of the matrix are exactly the given bases and the columns of the matrix are also bases. That is, it should be possible to find a second set of n disjoint bases Ci, each of which consists of one element from each of the bases Bi.
In mathematics, a matroid polytope, also called a matroid basis polytope to distinguish it from other polytopes derived from a matroid, is a polytope constructed via the bases of a matroid. Given a matroid , the matroid polytope is the convex hull of the indicator vectors of the bases of .
In mathematics, a basis of a matroid is a maximal independent set of the matroid—that is, an independent set that is not contained in any other independent set.























