Periodic systems of small molecules

Last updated

Periodic systems of molecules are charts of molecules similar to the periodic table of the elements. Construction of such charts was initiated in the early 20th century and is still ongoing.

Contents

It is commonly believed that the periodic law, represented by the periodic chart, is echoed in the behavior of molecules, at least small molecules. For instance, if one replaces any one of the atoms in a triatomic molecule with a rare gas atom, there will be a drastic change in the molecule’s properties. Several goals could be accomplished by constructing an explicit representation of this periodic law as manifested in molecules: (1) a classification scheme for the vast number of molecules that exist, starting with small ones having just a few atoms, for use as a teaching aid and tool for archiving data, (2) forecasting data for molecular properties based on the classification scheme, and (3) a sort of unity with the periodic chart and the periodic system of fundamental particles. [1]

Physical periodic systems of molecules

Periodic systems (or charts or tables) of molecules are the subjects of two reviews. [2] [3] The systems of diatomic molecules include those of (1) H. D. W. Clark, [4] [5] and (2) F.-A. Kong, [6] [7] which somewhat resemble the atomic chart. The system of R. Hefferlin et al. [8] [9] was developed from (3) a three-dimensional to (4) a four-dimensional system Kronecker product of the element chart with itself.

The Kronecker product of a hypothetical four-element periodic chart. The sixteen molecules, some of which are redundant, suggest a hypercube, which in turn suggests that the molecules exist in a four-dimensional space; the coordinates are the period numbers and group numbers of the two constituent atoms. [10]

A totally different kind of periodic system is (5) that of G. V. Zhuvikin, [11] [12] which is based on group dynamics. In all but the first of these cases, other researchers provided invaluable contributions and some of them are co-authors. The architectures of these systems have been adjusted by Kong [7] and Hefferlin [13] to include ionized species, and expanded by Kong, [7] Hefferlin, [9] and Zhuvikin and Hefferlin [12] to the space of triatomic molecules. These architectures are mathematically related to the chart of the elements. They were first called “physical” periodic systems. [2]

Chemical periodic systems of molecules

Other investigators have focused on building structures that address specific kinds of molecules such as alkanes (Morozov); [14] benzenoids (Dias); [15] [16] functional groups containing fluorine, oxygen, nitrogen and sulfur (Haas); [17] [18] or a combination of core charge, number of shells, redox potentials, and acid-base tendencies (Gorski). [19] [20] These structures are not restricted to molecules with a given number of atoms and they bear little resemblance to the element chart; they are called “chemical” systems. Chemical systems do not start with the element chart, but instead start with, for example, formula enumerations (Dias), Grimm's hydride displacement law (Haas), reduced potential curves (Jenz), [21] a set of molecular descriptors (Gorski), and similar strategies.

Hyperperiodicity

E. V. Babaev [22] has erected a hyperperiodic system which in principle includes all of the systems described above except those of Dias, Gorski, and Jenz.

Bases of the element chart and periodic systems of molecules

The periodic chart of the elements, like a small stool, is supported by three legs: (a) the Bohr–Sommerfeld “solar system” atomic model (with electron spin and the Madelung principle), which provides the magic-number elements that end each row of the table and gives the number of elements in each row, (b) solutions to the Schrödinger equation, which provide the same information, and (c) data provided by experiment, by the solar system model, and by solutions to the Schroedinger equation. The Bohr–Sommerfeld model should not be ignored: it gave explanations for the wealth of spectroscopic data that were already in existence before the advent of wave mechanics.

Each of the molecular systems listed above, and those not cited, is also supported by three legs: (a) physical and chemical data arranged in graphical or tabular patterns (which, for physical periodic systems at least, echo the appearance of the element chart), (b) group dynamic, valence-bond, molecular-orbital, and other fundamental theories, and (c) summing of atomic period and group numbers (Kong), the Kronecker product and exploitation of higher dimensions (Hefferlin), formula enumerations (Dias), the hydrogen-displacement principle (Haas), reduced potential curves (Jenz), and similar strategies.

A chronological list of the contributions to this field [3] contains almost thirty entries dated 1862, 1907, 1929, 1935, and 1936; then, after a pause, a higher level of activity beginning with the 100th anniversary of Mendeleev’s publication of his element chart, 1969. Many publications on periodic systems of molecules include some predictions of molecular properties, but starting at the turn of the Century there have been serious attempts to use periodic systems for the prediction of progressively more precise data for various numbers of molecules. Among these attempts are those of Kong, [7] and Hefferlin [23] [24]

A collapsed-coordinate system for triatomic molecules

The collapsed-coordinate system has three independent variables instead of the six demanded by the Kronecker-product system. The reduction of independent variables makes use of three properties of gas-phase, ground-state, triatomic molecules. (1) In general, whatever the total number of constituent atomic valence electrons, data for isoelectronic molecules tend to be more similar than for adjacent molecules that have more or fewer valence electrons; for triatomic molecules, the electron count is the sum of the atomic group numbers (the sum of the column numbers 1 to 8 in the p-block of the periodic chart of the elements, C1+C2+C3). (2) Linear/bent triatomic molecules appear to be slightly more stable, other parameters being equal, if carbon is the central atom. (3) Most physical properties of diatomic molecules (especially spectroscopic constants) are closely monotonic with respect to the product of the two atomic period (or row) numbers, R1 and R2; for triatomic molecules, the monotonicity is close with respect to R1R2+R2R3 (which reduces to R1R2 for diatomic molecules). Therefore, the coordinates x, y, and z of the collapsed-coordinate system are C1+C2+C3, C2, and R1R2+R2R3. Multiple-regression predictions of four property values for molecules with tabulated data agree very well with the tabulated data (the error measures of the predictions include the tabulated data in all but a few cases). [25]

See also

Related Research Articles

<span class="mw-page-title-main">Diatomic molecule</span> Molecule composed of any two atoms

Diatomic molecules are molecules composed of only two atoms, of the same or different chemical elements. If a diatomic molecule consists of two atoms of the same element, such as hydrogen or oxygen, then it is said to be homonuclear. Otherwise, if a diatomic molecule consists of two different atoms, such as carbon monoxide or nitric oxide, the molecule is said to be heteronuclear. The bond in a homonuclear diatomic molecule is non-polar.

Electronegativity, symbolized as χ, is the tendency for an atom of a given chemical element to attract shared electrons when forming a chemical bond. An atom's electronegativity is affected by both its atomic number and the distance at which its valence electrons reside from the charged nucleus. The higher the associated electronegativity, the more an atom or a substituent group attracts electrons. Electronegativity serves as a simple way to quantitatively estimate the bond energy, and the sign and magnitude of a bond's chemical polarity, which characterizes a bond along the continuous scale from covalent to ionic bonding. The loosely defined term electropositivity is the opposite of electronegativity: it characterizes an element's tendency to donate valence electrons.

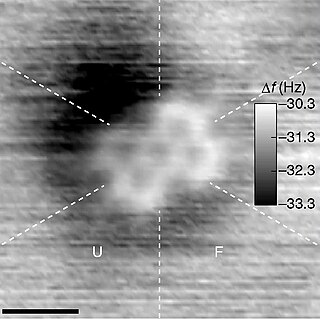
<span class="mw-page-title-main">Molecule</span> Electrically neutral group of two or more atoms

A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and biochemistry, the distinction from ions is dropped and molecule is often used when referring to polyatomic ions.

<span class="mw-page-title-main">Periodic table</span> Tabular arrangement of the chemical elements ordered by atomic number

The periodic table, also known as the periodic table of the elements, arranges the chemical elements into rows ("periods") and columns ("groups"). It is an icon of chemistry and is widely used in physics and other sciences. It is a depiction of the periodic law, which says that when the elements are arranged in order of their atomic numbers an approximate recurrence of their properties is evident. The table is divided into four roughly rectangular areas called blocks. Elements in the same group tend to show similar chemical characteristics.

Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of molecules, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed wave functions as well as to observable properties such as structures, spectra, and thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics.

The covalent radius, rcov, is a measure of the size of an atom that forms part of one covalent bond. It is usually measured either in picometres (pm) or angstroms (Å), with 1 Å = 100 pm.

<span class="mw-page-title-main">Ionization energy</span> Energy needed to remove an electron

In physics and chemistry, ionization energy (IE) (American English spelling), ionisation energy (British English spelling) is the minimum energy required to remove the most loosely bound electron of an isolated gaseous atom, positive ion, or molecule. The first ionization energy is quantitatively expressed as

<span class="mw-page-title-main">Electron configuration</span> Mode of arrangement of electrons in different shells of an atom

In atomic physics and quantum chemistry, the electron configuration is the distribution of electrons of an atom or molecule in atomic or molecular orbitals. For example, the electron configuration of the neon atom is 1s2 2s2 2p6, meaning that the 1s, 2s and 2p subshells are occupied by 2, 2 and 6 electrons respectively.

The van der Waals radius, rw, of an atom is the radius of an imaginary hard sphere representing the distance of closest approach for another atom. It is named after Johannes Diderik van der Waals, winner of the 1910 Nobel Prize in Physics, as he was the first to recognise that atoms were not simply points and to demonstrate the physical consequences of their size through the van der Waals equation of state.

A period 2 element is one of the chemical elements in the second row of the periodic table of the chemical elements. The periodic table is laid out in rows to illustrate recurring (periodic) trends in the chemical behavior of the elements as their atomic number increases; a new row is started when chemical behavior begins to repeat, creating columns of elements with similar properties.

In atomic physics, a partial charge is a non-integer charge value when measured in elementary charge units. It is represented by the Greek lowercase delta (𝛿), namely 𝛿− or 𝛿+.

A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunctions. In a mathematical sense, these wave functions are the basis set of functions, the basis functions, which describe the electrons of a given atom. In chemical reactions, orbital wavefunctions are modified, i.e. the electron cloud shape is changed, according to the type of atoms participating in the chemical bond.

In chemistry, molecular orbital theory is a method for describing the electronic structure of molecules using quantum mechanics. It was proposed early in the 20th century.

<span class="mw-page-title-main">VSEPR theory</span> Model for predicting molecular geometry

Valence shell electron pair repulsion (VSEPR) theory is a model used in chemistry to predict the geometry of individual molecules from the number of electron pairs surrounding their central atoms. It is also named the Gillespie-Nyholm theory after its two main developers, Ronald Gillespie and Ronald Nyholm.

In chemistry, orbital hybridisation is the concept of mixing atomic orbitals to form new hybrid orbitals suitable for the pairing of electrons to form chemical bonds in valence bond theory. For example, in a carbon atom which forms four single bonds the valence-shell s orbital combines with three valence-shell p orbitals to form four equivalent sp3 mixtures in a tetrahedral arrangement around the carbon to bond to four different atoms. Hybrid orbitals are useful in the explanation of molecular geometry and atomic bonding properties and are symmetrically disposed in space. Usually hybrid orbitals are formed by mixing atomic orbitals of comparable energies.

The atomic radius of a chemical element is the distance from the center of the nucleus to the outermost shell of an electron. Since the boundary is not a well-defined physical entity, there are various non-equivalent definitions of atomic radius. Depending on the definition, the term may apply only to isolated atoms, or also to atoms in condensed matter, covalently bound in molecules, or in ionized and excited states; and its value may be obtained through experimental measurements, or computed from theoretical models. Under some definitions, the value of the radius may depend on the atom's state and context.

A molecular orbital diagram, or MO diagram, is a qualitative descriptive tool explaining chemical bonding in molecules in terms of molecular orbital theory in general and the linear combination of atomic orbitals (LCAO) method in particular. A fundamental principle of these theories is that as atoms bond to form molecules, a certain number of atomic orbitals combine to form the same number of molecular orbitals, although the electrons involved may be redistributed among the orbitals. This tool is very well suited for simple diatomic molecules such as dihydrogen, dioxygen, and carbon monoxide but becomes more complex when discussing even comparatively simple polyatomic molecules, such as methane. MO diagrams can explain why some molecules exist and others do not. They can also predict bond strength, as well as the electronic transitions that can take place.

There are several known allotropes of oxygen. The most familiar is molecular oxygen, present at significant levels in Earth's atmosphere and also known as dioxygen or triplet oxygen. Another is the highly reactive ozone. Others are:

Atomicity is the total number of atoms present in a molecule of an element. For example, each molecule of oxygen (O2) is composed of two oxygen atoms. Therefore, the atomicity of oxygen is 2.

<span class="mw-page-title-main">FHI-aims</span> Molecular dynamics modelling software

FHI-aims is a software package for computational molecular and materials science written in Fortran. It uses density functional theory and many-body perturbation theory to simulate chemical and physical properties of atoms, molecules, nanostructures, solids, and surfaces. Originally developed at the Fritz Haber Institute in Berlin, the ongoing development of the FHI-aims source code is now driven by a worldwide community of collaborating research institutions.

References

  1. ↑ Chung, D.-Y. (2000). "The Periodic Table of Elementary Particles". arXiv: physics/0003023 .
  2. 1 2 Hefferlin, R. and Burdick, G.W. 1994. Fizicheskie i khimicheskie periodicheskie sistemy Molekul, Zhurnal Obshchei Xhimii, vol. 64, pp. 1870–1885. English translation: "Periodic Systems of Molecules: Physical and Chemical". Russ. J. Gen. Chem. 64: 1659–1674.
  3. 1 2 Hefferlin, R. 2006. The Periodic Systems of Molecules pp. 221 ff, in Baird, D., Scerri, E., and McIntyre, L. (Eds.) “The Philosophy of Chemistry, Synthesis of a New Discipline,” Springer, Dordrecht ISBN   1-4020-3256-0.
  4. ↑ Clark, C. H. D. (1935). "The periodic Groups of Non-Hydride Di-Atoms". Trans. Faraday Soc. 31: 1017–1036. doi:10.1039/tf9353101017.
  5. ↑ Clark, C. H. D (1940). "Systematics of Band-Spectral Constants. Part V. Interrelations of Dissociation Energy and Equilibrium Internuclear Distance of Di-Atoms in Ground States". Trans. Faraday Soc. 36: 370–376. doi:10.1039/tf9403500370.
  6. ↑ Kong, F (1982). "The Periodicity of Diatomic Molecules". J. Mol. Struct. 90: 17–28. Bibcode:1982JMoSt..90...17K. doi:10.1016/0022-2860(82)90199-5.
  7. 1 2 3 4 Kong, F. and Wu, W. 2010. Periodicity of Diatomic and Triatomic Molecules, Conference Proceedings of the 2010 Workshop on Mathematical Chemistry of the Americas.
  8. ↑ Hefferlin, R., Campbell, D. Gimbel, H. Kuhlman, and T. Cayton (1979). "The periodic table of diatomic molecules—I an algorithm for retrieval and prediction of spectrophysical properties". Quant. Spectrosc. Radiat. Transfer. 21 (4): 315–336. Bibcode:1979JQSRT..21..315H. doi:10.1016/0022-4073(79)90063-3.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  9. 1 2 Hefferlin, R (2008). "Kronecker-Product Periodic Systems of Small Gas-Phase Molecules and the Search for Order in Atomic Ensembles of Any Phase". Comb. Chem. High Throughput Screen. 11 (9): 690–706. doi:10.2174/138620708786306041. PMID   18991573.
  10. ↑ Gary W. Burdick and Ray Hefferlin, "Chapter 7. Data Location in a Four-Dimensional Periodic System of Diatomic Molecules", in Mihai V Putz, Ed., Chemical Information and Computational Challenges in the 21st Century, NOVA, 2011, ISBN   978-1-61209-712-1
  11. ↑ Zhuvikin, G.V. & R. Hefferlin (1983). "Periodicheskaya Sistema Dvukhatomnykh Molekul: Teoretiko-gruppovoi Podkhod, Vestnik Leningradskovo Universiteta" (16): 10–16.{{cite journal}}: Cite journal requires |journal= (help)
  12. 1 2 Carlson, C.M., Cavanaugh, R.J, Hefferlin, R.A, and of Zhuvikin, G.V. (1996). "Periodic Systems of Molecular States from the Boson Group Dynamics of SO(3)xSU(2)s". Chem. Inf. Comput. Sci. 36: 396–398. doi:10.1021/ci9500748.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  13. ↑ Hefferlin, R.; et al. (1984). "Periodic Systems of N-atom Molecules". J. Quant. Spectrosc. Radiat. Transfer. 32 (4): 257–268. Bibcode:1984JQSRT..32..257H. doi:10.1016/0022-4073(84)90098-0.
  14. ↑ Morozov, N. 1907. Stroeniya Veshchestva, I. D. Sytina Publication, Moscow.
  15. ↑ Dias, J.R. (1982). "A periodic Table of Polycyclic Aromatic Hydrocarbons. Isomer Enumeration of Fused Polycyclic Aromatic Hydrocarbons". Chem. Inf. Comput. Sci. 22: 15–22. doi:10.1021/ci00033a004.
  16. ↑ Dias, J. R. (1994). "Benzenoids to Fullerines and the Circumscribing and Leapfrog Algorithms". New J. Chem. 18: 667–673.
  17. ↑ Haas, A. (1982). "A new classification principle: the periodic system of functional groups". Chemiker-Zeitung. 106: 239–248.
  18. ↑ Haas, A. (1988). "Das Elementverscheibungsprinzip und siene Bedeutung fur die Chemie der p-Block Elemente". Kontakte (Darmstadt). 3: 3–11.
  19. ↑ Gorski, A (1971). "Morphological Classification of Simple Species. Part I. Fundamental Components of Chemical Structure". Roczniki Chemii. 45: 1981–1989.
  20. ↑ Gorski, A (1973). "Morphological Classification of Simple Species. Part V. Evaluation of Structural Parameters of Species". Roczniki Chemii. 47: 211–216.
  21. ↑ Jenz, F (1996). "The Reduced Potential Curve (RPC) Method and its Applications". Int. Rev. Phys. Chem. 15 (2): 467–523. Bibcode:1996IRPC...15..467J. doi:10.1080/01442359609353191.
  22. ↑ Babaev, E.V. and R. Hefferlin 1996. The Concepts of Periodicity and Hyper- periodicity: from Atoms to Molecules, in Rouvray, D.H. and Kirby, E.C., “Concepts in Chemistry,” Research Studies Press Limited, Taunton, Somerset, England.
  23. ↑ Hefferlin, R. (2010). "Vibration Frequencies using Least squares and Neural Networks for 50 new s and p Electron Diatomics". Quant. Spectr. Radiat. Transf. 111 (1): 71–77. Bibcode:2010JQSRT.111...71H. doi:10.1016/j.jqsrt.2009.08.004.
  24. ↑ Hefferlin, R. (2010). "Internuclear Separations using Least squares and Neural Networks for 46 new s and p Electron Diatomics".{{cite journal}}: Cite journal requires |journal= (help)
  25. ↑ Carlson, C., Gilkeson, J., Linderman, K., LeBlanc, S. Hefferlin, R., and Davis, B (1997). "Estimation of Properties of Triatomic Molecules from Tabulated Data Using Least-Squares Fitting". Croatica Chemica Acta. 70: 479–508.{{cite journal}}: CS1 maint: multiple names: authors list (link)
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.