
In geography, latitude is a geographic coordinate that specifies the north–south position of a point on the Earth's surface. Latitude is an angle which ranges from 0° at the Equator to 90° at the poles. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude is used together with longitude to specify the precise location of features on the surface of the Earth. On its own, the term latitude should be taken to be the geodetic latitude as defined below. Briefly, geodetic latitude at a point is the angle formed by the vector perpendicular to the ellipsoidal surface from that point, and the equatorial plane. Also defined are six auxiliary latitudes that are used in special applications.
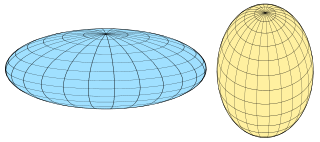
A spheroid, also known as an ellipsoid of revolution or rotational ellipsoid, is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters. A spheroid has circular symmetry.

An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

Earth radius is the distance from the center of Earth to a point on or near its surface. Approximating the figure of Earth by an Earth spheroid, the radius ranges from a maximum of nearly 6,378 km (3,963 mi) to a minimum of nearly 6,357 km (3,950 mi).

Hamiltonian mechanics emerged in 1833 as a reformulation of Lagrangian mechanics. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities used in Lagrangian mechanics with (generalized) momenta. Both theories provide interpretations of classical mechanics and describe the same physical phenomena.
In mathematics, the directional derivative of a multivariate differentiable (scalar) function along a given vector v at a given point x intuitively represents the instantaneous rate of change of the function, moving through x with a velocity specified by v.
In probability theory and statistics, the generalized extreme value (GEV) distribution is a family of continuous probability distributions developed within extreme value theory to combine the Gumbel, Fréchet and Weibull families also known as type I, II and III extreme value distributions. By the extreme value theorem the GEV distribution is the only possible limit distribution of properly normalized maxima of a sequence of independent and identically distributed random variables. Note that a limit distribution needs to exist, which requires regularity conditions on the tail of the distribution. Despite this, the GEV distribution is often used as an approximation to model the maxima of long (finite) sequences of random variables.
In physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are fixed in space. This problem is not exactly solvable, but yields an approximate solution for particles moving in the gravitational fields of prolate and oblate spheroids. This problem is named after Leonhard Euler, who discussed it in memoirs published in 1760. Important extensions and analyses were contributed subsequently by Lagrange, Liouville, Laplace, Jacobi, Darboux, Le Verrier, Velde, Hamilton, Poincaré, Birkhoff and E. T. Whittaker, among others.
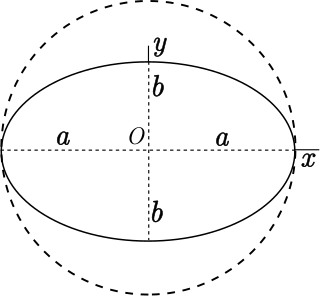
Flattening is a measure of the compression of a circle or sphere along a diameter to form an ellipse or an ellipsoid of revolution (spheroid) respectively. Other terms used are ellipticity, or oblateness. The usual notation for flattening is f and its definition in terms of the semi-axes of the resulting ellipse or ellipsoid is

The Universal Transverse Mercator (UTM) is a map projection system for assigning coordinates to locations on the surface of the Earth. Like the traditional method of latitude and longitude, it is a horizontal position representation, which means it ignores altitude and treats the earth as a perfect ellipsoid. However, it differs from global latitude/longitude in that it divides earth into 60 zones and projects each to the plane as a basis for its coordinates. Specifying a location means specifying the zone and the x, y coordinate in that plane. The projection from spheroid to a UTM zone is some parameterization of the transverse Mercator projection. The parameters vary by nation or region or mapping system.

The gravity of Earth, denoted by g, is the net acceleration that is imparted to objects due to the combined effect of gravitation and the centrifugal force.

Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the focal axis of the ellipse, i.e., the symmetry axis on which the foci are located. Rotation about the other axis produces oblate spheroidal coordinates. Prolate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two smallest principal axes are equal in length.

Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius in the x-y plane. Oblate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two largest semi-axes are equal in length.
Intrinsic viscosity is a measure of a solute's contribution to the viscosity of a solution. It should not be confused with inherent viscosity, which is the ratio of the natural logarithm of the relative viscosity to the mass concentration of the polymer.
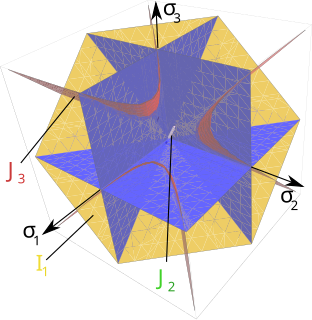
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the material is said to have become plastic. Further deformation of the material causes the stress state to remain on the yield surface, even though the shape and size of the surface may change as the plastic deformation evolves. This is because stress states that lie outside the yield surface are non-permissible in rate-independent plasticity, though not in some models of viscoplasticity.
Rotational diffusion is a process by which the equilibrium statistical distribution of the overall orientation of particles or molecules is maintained or restored. Rotational diffusion is the counterpart of translational diffusion, which maintains or restores the equilibrium statistical distribution of particles' position in space.
The prolate spheroidal wave functions are eigenfunctions of the Laplacian in prolate spheroidal coordinates, adapted to boundary conditions on certain ellipsoids of revolution. Related are the oblate spheroidal wave functions.
In mathematical physics, the Berezin integral, named after Felix Berezin,, is a way to define integration for functions of Grassmann variables. It is not an integral in the Lebesgue sense; the word "integral" is used because the Berezin integral has properties analogous to the Lebesgue integral and because it extends the path integral in physics, where it is used as a sum over histories for fermions.
Nodal precession is the precession of the orbital plane of a satellite around the rotational axis of an astronomical body such as Earth. This precession is due to the non-spherical nature of a rotating body, which creates a non-uniform gravitational field. The following discussion relates to low Earth orbit of artificial satellites, which have no measurable effect on the motion of Earth. The nodal precession of more massive, natural satellites like the Moon is more complex.
In applied mathematics, oblate spheroidal wave functions are involved in the solution of the Helmholtz equation in oblate spheroidal coordinates. When solving this equation, , by the method of separation of variables, , with:




































