A major contributor to this article appears to have a close connection with its subject.(December 2011) |
Peter Kramer (born 1933 in Quedlinburg) is a German physicist.
A major contributor to this article appears to have a close connection with its subject.(December 2011) |
Peter Kramer (born 1933 in Quedlinburg) is a German physicist.
Kramer studied physics at the University of Münster, the University of Tübingen, the University of Bristol and the University of Marburg. He received his PhD in 1964 in Marburg and in 1968 his Habilitation in Tübingen. He was a postdoc at the UNAM in Mexico City, where he collaborated with Marcos Moshinsky. He was a professor at the Institute for Theoretical Physics in Tübingen from 1970 until 1998 when he retired. He has also served as a Dean and a Vice President at the University of Tübingen. Kramer married in 1962 and has two children.
Kramer's work is concerned with applications of groups and representations in mathematical physics. His early work was in nuclear physics. In the early eighties he and his student Roberto Neri developed a mathematical model for quasiperiodic tesselations of three-dimensional space. Their paper was submitted in 1983 and published in 1984, [1] the same year that Dan Shechtman and his co-workers announced the experimental discovery of an alloy with icosahedral quasi-crystalline structure. [2] [3] Shechtman was awarded the 2011 Nobel Prize in chemistry for his work.
More recently, Kramer has become interested in cosmology and three-dimensional space forms. His scientific œuvre contains more than 200 publications. [4]

Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases, that arise from electromagnetic forces between atoms and electrons. More generally, the subject deals with condensed phases of matter: systems of many constituents with strong interactions among them. More exotic condensed phases include the superconducting phase exhibited by certain materials at extremely low cryogenic temperatures, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, the Bose–Einstein condensates found in ultracold atomic systems, and liquid crystals. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other physics theories to develop mathematical models and predict the properties of extremely large groups of atoms.

A quasiperiodic crystal, or quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry. While crystals, according to the classical crystallographic restriction theorem, can possess only two-, three-, four-, and six-fold rotational symmetries, the Bragg diffraction pattern of quasicrystals shows sharp peaks with other symmetry orders—for instance, five-fold.

Quantum chaos is a branch of physics focused on how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is: "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle states that classical mechanics is the classical limit of quantum mechanics, specifically in the limit as the ratio of the Planck constant to the action of the system tends to zero. If this is true, then there must be quantum mechanisms underlying classical chaos. If quantum mechanics does not demonstrate an exponential sensitivity to initial conditions, how can exponential sensitivity to initial conditions arise in classical chaos, which must be the correspondence principle limit of quantum mechanics?

In quantum physics and chemistry, quantum numbers are quantities that characterize the possible states of the system. To fully specify the state of the electron in a hydrogen atom, four quantum numbers are needed. The traditional set of quantum numbers includes the principal, azimuthal, magnetic, and spin quantum numbers. To describe other systems, different quantum numbers are required. For subatomic particles, one needs to introduce new quantum numbers, such as the flavour of quarks, which have no classical correspondence.
The year 1984 in science and technology involved some significant events.

An aperiodic tiling is a non-periodic tiling with the additional property that it does not contain arbitrarily large periodic regions or patches. A set of tile-types is aperiodic if copies of these tiles can form only non-periodic tilings.

In atomic physics and quantum chemistry, the Aufbau principle, also called the Aufbau rule, states that in the ground state of an atom or ion, electrons first fill subshells of the lowest available energy, then fill subshells of higher energy. For example, the 1s subshell is filled before the 2s subshell is occupied. In this way, the electrons of an atom or ion form the most stable electron configuration possible. An example is the configuration 1s2 2s2 2p6 3s2 3p3 for the phosphorus atom, meaning that the 1s subshell has 2 electrons, the 2s subshell has 2 electrons, the 2p subshell has 6 electrons, and so on.
Paul Joseph Steinhardt is an American theoretical physicist whose principal research is in cosmology and condensed matter physics. He is currently the Albert Einstein Professor in Science at Princeton University, where he is on the faculty of both the Departments of Physics and of Astrophysical Sciences.

In particle physics, the history of quantum field theory starts with its creation by Paul Dirac, when he attempted to quantize the electromagnetic field in the late 1920s. Major advances in the theory were made in the 1940s and 1950s, leading to the introduction of renormalized quantum electrodynamics (QED). The field theory behind QED was so accurate and successful in predictions that efforts were made to apply the same basic concepts for the other forces of nature. Beginning in 1954, the parallel was found by way of gauge theory, leading by the late 1970s, to quantum field models of strong nuclear force and weak nuclear force, united in the modern Standard Model of particle physics.
In theoretical physics, thermal quantum field theory or finite temperature field theory is a set of methods to calculate expectation values of physical observables of a quantum field theory at finite temperature.

Dan Shechtman is the Philip Tobias Professor of Materials Science at the Technion – Israel Institute of Technology, an Associate of the US Department of Energy's Ames National Laboratory, and Professor of Materials Science at Iowa State University. On April 8, 1982, while on sabbatical at the U.S. National Bureau of Standards in Washington, D.C., Shechtman discovered the icosahedral phase, which opened the new field of quasiperiodic crystals.
In physics, a phason is a form of collective excitation found in aperiodic crystal structures. Phasons are a type of quasiparticle: an emergent phenomenon of many-particle systems. The phason can also be seen as a degree of freedom unique to quasicrystals. Similar to phonons, phasons are quasiparticles associated with atomic motion. However, whereas phonons are related to the translation of atoms, phasons are associated with atomic rearrangement. As a result of this rearrangement, or modulation, the waves that describe the position of atoms in the crystal change phase -- hence the term "phason". In the language of the superspace picture commonly employed in the description of aperiodic crystals in which the aperiodic function is obtained via projection from a higher dimensional periodic function, the 'phason' displacement can be seen as displacement of the (higher-dimensional) lattice points in the perpendicular space.

In condensed matter physics, a time crystal is a quantum system of particles whose lowest-energy state is one in which the particles are in repetitive motion. The system cannot lose energy to the environment and come to rest because it is already in its quantum ground state. Time crystals were first proposed theoretically by Frank Wilczek in 2012 as a time-based analogue to common crystals – whereas the atoms in crystals are arranged periodically in space, the atoms in a time crystal are arranged periodically in both space and time. Several different groups have demonstrated matter with stable periodic evolution in systems that are periodically driven. In terms of practical use, time crystals may one day be used as quantum computer memory.

Alan Lindsay Mackay FRS is a British crystallographer, born in Wolverhampton.

An icosahedral twin is a nanostructure found in atomic clusters and also nanoparticles with some thousands of atoms. These clusters are twenty-faced, with twenty interlinked tetrahedral crystals joined along triangular faces having three-fold symmetry. A related, more common structure has five units similarly arranged with twinning, which were known as "fivelings" in the 19th century, more recently as "decahedral multiply twinned particles", "pentagonal particles" or "star particles". A variety of different methods lead to the icosahedral form at size scales where surface energies are more important than those from the bulk.
In solid state physics, the magnetic space groups, or Shubnikov groups, are the symmetry groups which classify the symmetries of a crystal both in space, and in a two-valued property such as electron spin. To represent such a property, each lattice point is colored black or white, and in addition to the usual three-dimensional symmetry operations, there is a so-called "antisymmetry" operation which turns all black lattice points white and all white lattice points black. Thus, the magnetic space groups serve as an extension to the crystallographic space groups which describe spatial symmetry alone.

Theo Willem Jan Marie Janssen, better known as Ted Janssen, was a Dutch physicist and Full Professor of Theoretical Physics at the Radboud University Nijmegen. Together with Pim de Wolff and Aloysio Janner, he was one of the founding fathers of N-dimensional superspace approach in crystal structure analysis for the description of quasi periodic crystals and modulated structures. For this work he received the Aminoff Prize of the Royal Swedish Academy of Sciences in 1988 and the Ewald Prize of the International Union of Crystallography in 2014. These achievements were merit of his unique talent, combining a deep knowledge of physics with a rigorous mathematical approach. Their theoretical description of the structure and symmetry of incommensurate crystals using higher dimensional superspace groups also included the quasicrystals that were discovered in 1982 by Dan Schechtman, who received the Nobel Prize in Chemistry in 2011. The Swedish Academy of Sciences explicitly mentioned their work at this occasion.
Werner Fischer is a German mineralogist and mathematical crystallographer.
Dov I. Levine is an American-Israeli physicist, known for his research on quasicrystals, soft condensed matter physics, and statistical mechanics out of equilibrium.
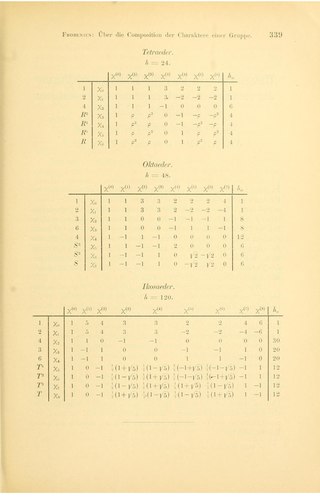
In applied mathematics, finite subgroups of SU(2) are groups composed of rotations and related transformations, employed particularly in the field of physical chemistry. The symmetry group of a physical body generally contains a subgroup of the 3D rotation group. It may occur that the group {±1} with two elements acts also on the body; this is typically the case in magnetism for the exchange of north and south poles, or in quantum mechanics for the change of spin sign. In this case, the symmetry group of a body may be a central extension of the group of spatial symmetries by the group with two elements. Hans Bethe introduced the term "double group" (Doppelgruppe) for such a group, in which two different elements induce the spatial identity, and a rotation of 2π may correspond to an element of the double group that is not the identity.