Related Research Articles
In chemistry, the mesomeric effect is a property of substituents or functional groups in a chemical compound. It is defined as the polarity produced in the molecule by the interaction of two pi bonds or between a pi bond and lone pair of electrons present on an adjacent atom. This change in electron arrangement results in the formation of resonance structures that hybridize into the molecule's true structure. The pi electrons then move away from or toward a particular substituent group. The mesomeric effect is stronger in compounds with a lower ionization potential. This is because the electron transfer states will have lower energies.

In theoretical chemistry, a conjugated system is a system of connected p-orbitals with delocalized electrons in a molecule, which in general lowers the overall energy of the molecule and increases stability. It is conventionally represented as having alternating single and multiple bonds. Lone pairs, radicals or carbenium ions may be part of the system, which may be cyclic, acyclic, linear or mixed. The term "conjugated" was coined in 1899 by the German chemist Johannes Thiele.
In chemistry, resonance, also called mesomerism, is a way of describing bonding in certain molecules or polyatomic ions by the combination of several contributing structures into a resonance hybrid in valence bond theory. It has particular value for analyzing delocalized electrons where the bonding cannot be expressed by one single Lewis structure. The resonance hybrid is the accurate structure for a molecule or ion; it is an average of the theoretical contributing structures.
In electrophilic aromatic substitution reactions, existing substituent groups on the aromatic ring influence the overall reaction rate or have a directing effect on positional isomer of the products that are formed.

In organic chemistry, hyperconjugation refers to the delocalization of electrons with the participation of bonds of primarily σ-character. Usually, hyperconjugation involves the interaction of the electrons in a sigma (σ) orbital with an adjacent unpopulated non-bonding p or antibonding σ* or π* orbitals to give a pair of extended molecular orbitals. However, sometimes, low-lying antibonding σ* orbitals may also interact with filled orbitals of lone pair character (n) in what is termed negative hyperconjugation. Increased electron delocalization associated with hyperconjugation increases the stability of the system. In particular, the new orbital with bonding character is stabilized, resulting in an overall stabilization of the molecule. Only electrons in bonds that are in the β position can have this sort of direct stabilizing effect — donating from a sigma bond on an atom to an orbital in another atom directly attached to it. However, extended versions of hyperconjugation can be important as well. The Baker–Nathan effect, sometimes used synonymously for hyperconjugation, is a specific application of it to certain chemical reactions or types of structures.
In Organic chemistry, the inductive effect in a molecule is a local change in the electron density due to electron-withdrawing or electron-donating groups elsewhere in the molecule, resulting in a permanent dipole in a bond. It is present in a σ (sigma) bond, unlike the electromeric effect which is present in a π (pi) bond.
The Hückel method or Hückel molecular orbital theory, proposed by Erich Hückel in 1930, is a simple method for calculating molecular orbitals as linear combinations of atomic orbitals. The theory predicts the molecular orbitals for π-electrons in π-delocalized molecules, such as ethylene, benzene, butadiene, and pyridine. It provides the theoretical basis for Hückel's rule that cyclic, planar molecules or ions with π-electrons are aromatic. It was later extended to conjugated molecules such as pyridine, pyrrole and furan that contain atoms other than carbon and hydrogen (heteroatoms). A more dramatic extension of the method to include σ-electrons, known as the extended Hückel method (EHM), was developed by Roald Hoffmann. The extended Hückel method gives some degree of quantitative accuracy for organic molecules in general and was used to provide computational justification for the Woodward–Hoffmann rules. To distinguish the original approach from Hoffmann's extension, the Hückel method is also known as the simple Hückel method (SHM).
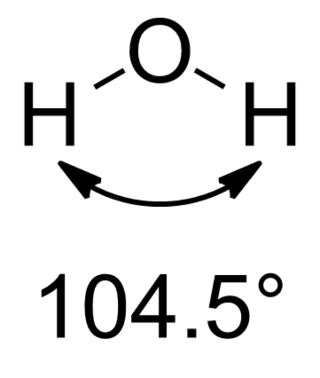
In chemistry, Bent's rule describes and explains the relationship between the orbital hybridization and the electronegativities of substituents. The rule was stated by Henry A. Bent as follows:
Atomic s character concentrates in orbitals directed toward electropositive substituents.
An electron-withdrawing group (EWG) is a group or atom that has the ability to draw electron density toward itself and away from other adjacent atoms. This electron density transfer is often achieved by resonance or inductive effects. Electron-withdrawing groups have significant impacts on fundamental chemical processes such as acid-base reactions, redox potentials, and substitution reactions.
In organic chemistry, the Hammett equation describes a linear free-energy relationship relating reaction rates and equilibrium constants for many reactions involving benzoic acid derivatives with meta- and para-substituents to each other with just two parameters: a substituent constant and a reaction constant. This equation was developed and published by Louis Plack Hammett in 1937 as a follow-up to qualitative observations in his 1935 publication.
Physical organic chemistry, a term coined by Louis Hammett in 1940, refers to a discipline of organic chemistry that focuses on the relationship between chemical structures and reactivity, in particular, applying experimental tools of physical chemistry to the study of organic molecules. Specific focal points of study include the rates of organic reactions, the relative chemical stabilities of the starting materials, reactive intermediates, transition states, and products of chemical reactions, and non-covalent aspects of solvation and molecular interactions that influence chemical reactivity. Such studies provide theoretical and practical frameworks to understand how changes in structure in solution or solid-state contexts impact reaction mechanism and rate for each organic reaction of interest.
The Taft equation is a linear free energy relationship (LFER) used in physical organic chemistry in the study of reaction mechanisms and in the development of quantitative structure–activity relationships for organic compounds. It was developed by Robert W. Taft in 1952 as a modification to the Hammett equation. While the Hammett equation accounts for how field, inductive, and resonance effects influence reaction rates, the Taft equation also describes the steric effects of a substituent. The Taft equation is written as:
An electric effect influences the structure, reactivity, or properties of a molecule but is neither a traditional bond nor a steric effect. In organic chemistry, the term stereoelectronic effect is also used to emphasize the relation between the electronic structure and the geometry (stereochemistry) of a molecule.
In physical organic chemistry, the Swain–Lupton equation is a linear free energy relationship (LFER) that is used in the study of reaction mechanisms and in the development of quantitative structure activity relationships for organic compounds. It was developed by C. Gardner Swain and Elmer C. Lupton Jr. in 1968 as a refinement of the Hammett equation to include both field effects and resonance effects.
The Yukawa–Tsuno equation, first developed in 1959, is a linear free-energy relationship in physical organic chemistry. It is a modified version of the Hammett equation that accounts for enhanced resonance effects in electrophilic reactions of para- and meta-substituted organic compounds. This equation does so by introducing a new term to the original Hammett relation that provides a measure of the extent of resonance stabilization for a reactive structure that builds up charge in its transition state. The Yukawa–Tsuno equation can take the following forms:
Electrophilic aromatic substitution (SEAr) is an organic reaction in which an atom that is attached to an aromatic system is replaced by an electrophile. Some of the most important electrophilic aromatic substitutions are aromatic nitration, aromatic halogenation, aromatic sulfonation, alkylation Friedel–Crafts reaction and acylation Friedel–Crafts reaction.
In chemistry, primarily organic and computational chemistry, a stereoelectronic effect is an effect on molecular geometry, reactivity, or physical properties due to spatial relationships in the molecules' electronic structure, in particular the interaction between atomic and/or molecular orbitals. Phrased differently, stereoelectronic effects can also be defined as the geometric constraints placed on the ground and/or transition states of molecules that arise from considerations of orbital overlap. Thus, a stereoelectronic effect explains a particular molecular property or reactivity by invoking stabilizing or destabilizing interactions that depend on the relative orientations of electrons in space.
In organic chemistry, the Cieplak effect is a predictive model to rationalize why nucleophiles preferentially add to one face of a carbonyl over another. Proposed by Andrzej Stanislaw Cieplak in 1980, it correctly predicts results that could not be justified by the other standard models at the time, such as the Cram and Felkin–Anh models. In the Cieplak model, electrons from a neighboring bond delocalize into the forming carbon–nucleophile (C–Nuc) bond, lowering the energy of the transition state and accelerating the rate of reaction. Whichever bond can best donate its electrons into the C–Nuc bond determines which face of the carbonyl the nucleophile will add to. The nucleophile may be any of a number of reagents, most commonly organometallic or reducing agents. The Cieplak effect is subtle, and often competes with sterics, solvent effects, counterion complexation of the carbonyl oxygen, and other effects to determine product distribution. Subsequent work has questioned its legitimacy.

In chemistry, pi stacking refers to the presumptive attractive, noncovalent pi interactions between the pi bonds of aromatic rings. According to some authors direct stacking of aromatic rings is electrostatically repulsive.
The sEDA parameter is a sigma-electron substituent effect scale, described also as inductive and electronegativity related effect. There is also a complementary scale - pEDA. The more positive is the value of sEDA the more sigma-electron donating is a substituent. The more negative sEDA, the more sigma-electron withdrawing is the substituent.
References
- ↑ Ozimiński, Wojciech P.; Dobrowolski, Jan C. (2009-08-01). "σ- and π-electron contributions to the substituent effect: natural population analysis". Journal of Physical Organic Chemistry. 22 (8): 769–778. doi:10.1002/poc.1530. ISSN 1099-1395.
- ↑ R. W. Taft, R. D. Topsom (1987). Prog. Phys. Org. Chem. 16. pp. 1–83.
{{cite book}}: CS1 maint: location (link) CS1 maint: location missing publisher (link)