The erlang is a dimensionless unit that is used in telephony as a measure of offered load or carried load on service-providing elements such as telephone circuits or telephone switching equipment. A single cord circuit has the capacity to be used for 60 minutes in one hour. Full utilization of that capacity, 60 minutes of traffic, constitutes 1 erlang.
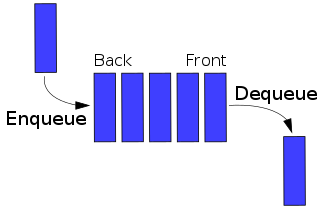
In computing and in systems theory, FIFO is an acronym for first in, first out, a method for organizing the manipulation of a data structure where the oldest (first) entry, or "head" of the queue, is processed first.

Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world.
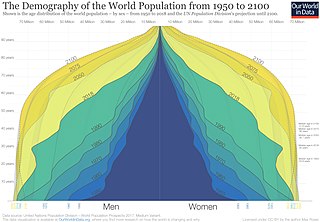
Demography is the statistical study of populations, especially human beings.

Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service.

A system on a chip or system-on-chip is an integrated circuit that integrates most or all components of a computer or other electronic system. These components almost always include on-chip central processing unit (CPU), memory interfaces, input/output devices, input/output interfaces, and secondary storage interfaces, often alongside other components such as radio modems and a graphics processing unit (GPU) – all on a single substrate or microchip. It may contain digital, and also analog, mixed-signal, and often radio frequency signal processing functions.

Toxicity is the degree to which a chemical substance or a particular mixture of substances can damage an organism. Toxicity can refer to the effect on a whole organism, such as an animal, bacterium, or plant, as well as the effect on a substructure of the organism, such as a cell (cytotoxicity) or an organ such as the liver (hepatotoxicity). By extension, the word may be metaphorically used to describe toxic effects on larger and more complex groups, such as the family unit or society at large. Sometimes the word is more or less synonymous with poisoning in everyday usage.

Population ecology is a sub-field of ecology that deals with the dynamics of species populations and how these populations interact with the environment, such as birth and death rates, and by immigration and emigration.
Civil registration is the system by which a government records the vital events of its citizens and residents. The resulting repository or database has different names in different countries and even in different US states. It can be called a civil registry, civil register, vital records, and other terms, and the office responsible for receiving the registrations can be called a bureau of vital statistics, registry of vital records and statistics, registrar, registry, register, registry office, or population registry. The primary purpose of civil registration is to create a legal document that can be used to establish and protect the rights of individuals. A secondary purpose is to create a data source for the compilation of vital statistics.
The birth–death process is a special case of continuous-time Markov process where the state transitions are of only two types: "births", which increase the state variable by one and "deaths", which decrease the state by one. It was introduced by William Feller. The model's name comes from a common application, the use of such models to represent the current size of a population where the transitions are literal births and deaths. Birth–death processes have many applications in demography, queueing theory, performance engineering, epidemiology, biology and other areas. They may be used, for example, to study the evolution of bacteria, the number of people with a disease within a population, or the number of customers in line at the supermarket.

The dose–response relationship, or exposure–response relationship, describes the magnitude of the response of an organism, as a function of exposure to a stimulus or stressor after a certain exposure time. Dose–response relationships can be described by dose–response curves. This is explained further in the following sections. A stimulus response function or stimulus response curve is defined more broadly as the response from any type of stimulus, not limited to chemicals.
A discrete-event simulation (DES) models the operation of a system as a (discrete) sequence of events in time. Each event occurs at a particular instant in time and marks a change of state in the system. Between consecutive events, no change in the system is assumed to occur; thus the simulation time can directly jump to the occurrence time of the next event, which is called next-event time progression.

In queueing theory, a discipline within the mathematical theory of probability, Kendall's notation is the standard system used to describe and classify a queueing node. D. G. Kendall proposed describing queueing models using three factors written A/S/c in 1953 where A denotes the time between arrivals to the queue, S the service time distribution and c the number of service channels open at the node. It has since been extended to A/S/c/K/N/D where K is the capacity of the queue, N is the size of the population of jobs to be served, and D is the queueing discipline.
In queueing theory, a discipline within the mathematical theory of probability, Burke's theorem is a theorem asserting that, for the M/M/1 queue, M/M/c queue or M/M/∞ queue in the steady state with arrivals is a Poisson process with rate parameter λ:
- The departure process is a Poisson process with rate parameter λ.
- At time t the number of customers in the queue is independent of the departure process prior to time t.
In queueing theory, a discipline within the mathematical theory of probability, the M/M/c queue is a multi-server queueing model. In Kendall's notation it describes a system where arrivals form a single queue and are governed by a Poisson process, there are c servers, and job service times are exponentially distributed. It is a generalisation of the M/M/1 queue which considers only a single server. The model with infinitely many servers is the M/M/∞ queue.
Toxic equivalency factor (TEF) expresses the toxicity of dioxins, furans and PCBs in terms of the most toxic form of dioxin, 2,3,7,8-TCDD. The toxicity of the individual congeners may vary by orders of magnitude.

Sri Lankan passports are issued to citizens of Sri Lanka for the purpose of international travel. The Department of Immigration and Emigration is responsible for issuing Sri Lankan passports.
In queueing theory, a discipline within the mathematical theory of probability, an M/G/1 queue is a queue model where arrivals are Markovian, service times have a General distribution and there is a single server. The model name is written in Kendall's notation, and is an extension of the M/M/1 queue, where service times must be exponentially distributed. The classic application of the M/G/1 queue is to model performance of a fixed head hard disk.
This glossary of biology terms is a list of definitions of fundamental terms and concepts used in biology, the study of life and of living organisms. It is intended as introductory material for novices; for more specific and technical definitions from sub-disciplines and related fields, see Glossary of genetics, Glossary of evolutionary biology, Glossary of ecology, and Glossary of scientific naming, or any of the organism-specific glossaries in Category:Glossaries of biology.
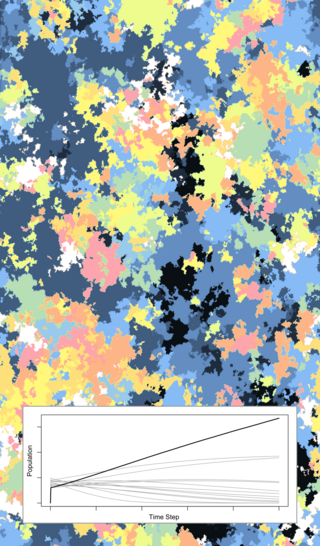
Microscale models form a broad class of computational models that simulate fine-scale details, in contrast with macroscale models, which amalgamate details into select categories. Microscale and macroscale models can be used together to understand different aspects of the same problem.










