This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these template messages) (Learn how and when to remove this template message)
|
In economics, price dispersion is variation in prices across sellers of the same item, holding fixed the item's characteristics. Price dispersion can be viewed as a measure of trading frictions (or, tautologically, as a violation of the law of one price). It is often attributed to consumer search costs or unmeasured attributes (such as the reputation) of the retailing outlets involved. There is a difference between price dispersion and price discrimination. The latter concept involves a single provider charging different prices to different customers for an identical good. Price dispersion, on the other hand, is best thought of as the outcome of many firms potentially charging different prices, where customers of one firm find it difficult to patronize (or are perhaps unaware of) other firms due to the existence of search costs.

Economics is the social science that studies the production, distribution, and consumption of goods and services.
The law of one price (LOOP) states that in the absence of trade frictions, and under conditions of free competition and price flexibility, identical goods sold in different locations must sell for the same price when prices are expressed in a common currency. This law is derived from the assumption of the inevitable elimination of all arbitrage.
In microeconomics, search theory studies buyers or sellers who cannot instantly find a trading partner, and must therefore search for a partner prior to transacting.
Contents
- Consumer search and price dispersion
- Search alone is insufficient
- A necessary condition
- Price dispersion in a non-sequential search model
- Price dispersion in a sequential search model
- See also
- References
Price dispersion measures include the range of prices, the percentage difference of highest and lowest price, the standard deviation of the price distribution, the variance of the price distribution, and the coefficient of variation of the price distribution.
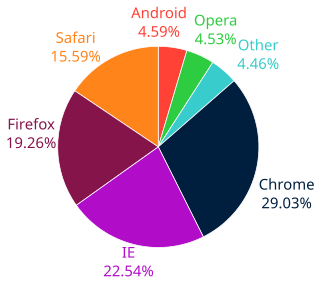
In mathematics, a percentage is a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign, "%", or the abbreviations "pct.", "pct"; sometimes the abbreviation "pc" is also used. A percentage is a dimensionless number.

In statistics, the standard deviation is a measure that is used to quantify the amount of variation or dispersion of a set of data values. A low standard deviation indicates that the data points tend to be close to the mean of the set, while a high standard deviation indicates that the data points are spread out over a wider range of values.

In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its mean. Informally, it measures how far a set of (random) numbers are spread out from their average value. Variance has a central role in statistics, where some ideas that use it include descriptive statistics, statistical inference, hypothesis testing, goodness of fit, and Monte Carlo sampling. Variance is an important tool in the sciences, where statistical analysis of data is common. The variance is the square of the standard deviation, the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by , , or .
In most theoretical literature, price dispersion is argued as result from spatial difference and the existence of significant search cost. With the development of internet and shopping agent programs, conventional wisdom tells that price dispersion should be alleviated and may eventually disappear in the online market due to the reduced search cost for both price and product features. However, recent studies found a surprisingly high level of price dispersion online, even for standardized items such as books, CDs and DVDs. There is some evidence of a shrinking of this online price dispersion, but it remains significant. Recently, work has also been done in the area of e-commerce, specifically the Semantic Web, and its effects on price dispersion.
Hal Varian, an economist at U. C. Berkeley, argued in a 1980 article that price dispersion may be an intentional marketing technique to encourage shoppers to explore their options. [1]

Hal Ronald Varian is an economist specializing in microeconomics and information economics. He is the chief economist at Google and he holds the title of emeritus professor at the University of California, Berkeley where he was founding dean of the School of Information.
A related concept is that of wage dispersion.